在网上看到过图片系列,名字叫做 不需要文字的数学证明,或者叫做 怪不得我数学没学好 一类的。用静止图片或者动图展示数学原理。例如 用三角形边长构成正方形,灌上水,用水的体积用面积相等验证勾股定理;圆旋转,把圆周上的点沿横坐标延开演示正弦曲线的。印象挺深的一个动图,是用大圆上套小圆,三个圆吧,展示方波的傅里叶分解。感觉非常炫酷,值得照着做一个。
仿制的方法和过程如下,用 geogebra实现。个别细节需要Excel,并非必须也可以用其他工具代替。
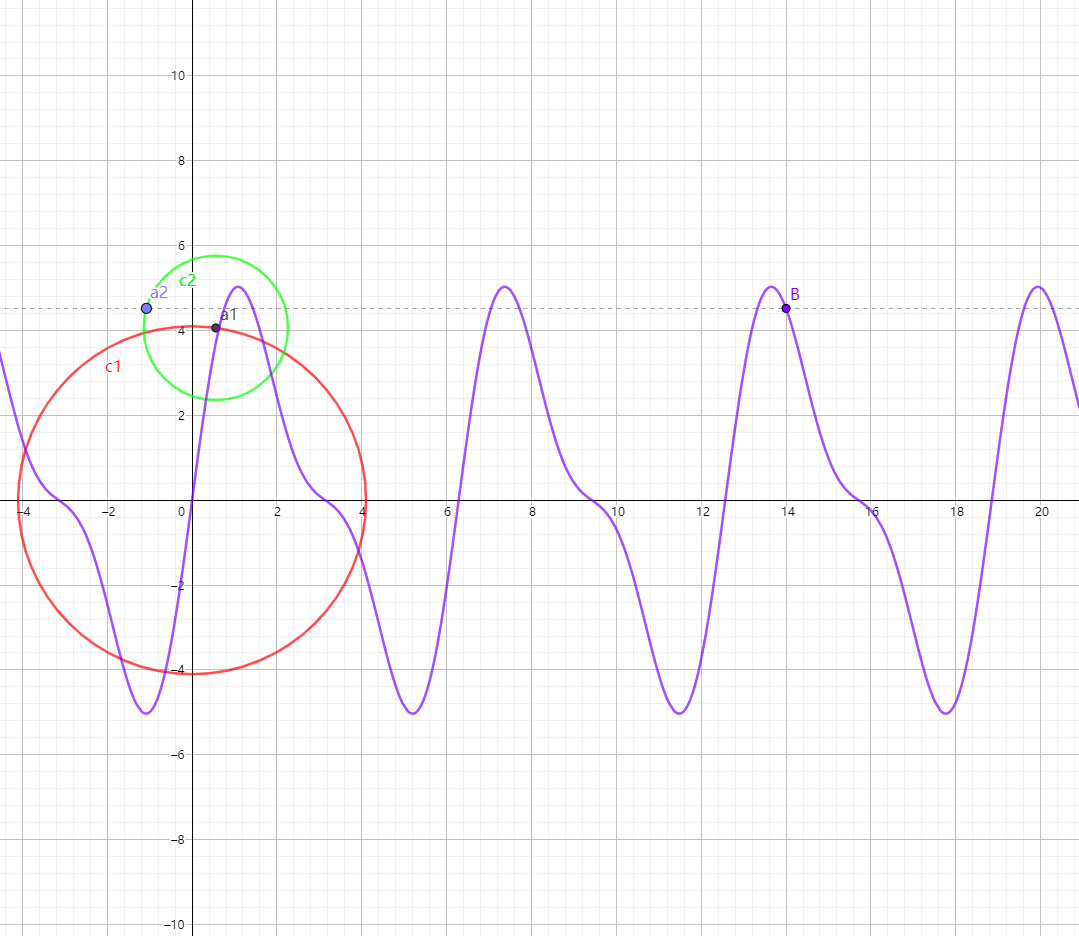
最终效果大致如下面的效果图所示。

图中,要傅里叶分解画出的曲线是浅灰色的细线,大致呈现方波的形状。有3个圆,不同的半径(以及初始相位)“拟合”出方波。这三个圆从大到小,分别为 红色、绿色、蓝色。第一个即红色圆上的一点,作为第二个即绿色圆的圆心;第二个即绿色圆上的一点,作为第三个即蓝色圆的圆心。当红、绿、蓝三个圆按各自不同的固定周期旋转时,运动叠加的结果在横坐标上展开,刚好符合方波的函数图像。
这个 geogebra 项目完成后能够画出的任意函数图形,不止限于方波。
1. 需要的技术及原型
考虑效果图所呈现的元素,以及各元素间的关联,可以得出需要哪些geogebra中的技术。
最核心的效果,是一个绿圆上,以另一个红圆作为圆心。或者更完整的表述,应该是 一个绿圆上的点,以另一个红圆上的点作为圆心。这样,就能逐级完成傅里叶级数的累加。
我们从简单的开始,不需要 geogebra 基本也容易理解。如果某个技术不熟悉,也容易单独做个 geogebra 小项目测试一下。
1.1 第一个圆,指定圆心和半径
第一个圆分成两部分,一是 圆周,二是 圆周上的点。
圆周 的定义如下。
![]()
我们把圆心设置在原点 (0,0)位置,半径为r1。这样,就自动得到了变量r1,如下。我们随便设置半径r1的值,以后会经常调整它的值。

圆周上的点 定义如下。

横坐标为半径r1乘以角度alpha1的余弦值,
纵坐标为半径r1乘以角度alpha1的正弦值。
这正符合余弦和正弦在单位圆中的定义。
我们在圆周上的点的定义中使用了刚才定义的变量 半径r1,并且自动得到了另一个变量 角度 alpha1。角度的值在以后也会经常调整。
以上,由圆周和圆周上的点,我们得到了第一个圆。如下图所示。

1.2 行星轨道
通过下图中红箭头所指的单选按钮,把 r1 和 alpha1 的 滑动条slide 显示在屏幕上。在setting中可以指定slide的范围。

拖动 alpha1 或 r1,可以得到半径不同的圆,以及 不同角度的a1。如下图所示。


如果把原点视为太阳,c1是行星的轨道,a1是轨道上的行星。这个比喻有利于观看动图的人更易于理解我们的意图。
1.3 第二个圆
第二个圆也由两部分需要讨论,一是圆周,二是圆周上的点,如下图所示。

从上图可以看出,第一个圆的圆心有固定坐标(0,0),而第二个圆的圆心不是固定的。第二个圆的圆心是第一个圆圆周上的点a1,这个点a1受r1和theta1两个变量的影响。在最终的成品中,我们会注意到,不同的级别有不同的半径,并且演示傅里叶级数的过程中,角度是一直在变动的。
第二个圆的圆周,圆心是a1,半径是变量r2。

第二个圆的圆周的上的点,如下。

横坐标为 圆心a1的横坐标x(a1) 加上 半径r2 乘以 alpha2的余弦。同理,得到纵坐标。
1.4 卫星轨道
在以后的完整项目中,调整两个圆的半径,对应了傅里叶变换不同级数的系数Cn.在这里,可以手动调节r1和r2两个滑动条,查看c1和c2。下面的三张图,展示了不同半径对比,红圆的半径是r1,绿圆的半径是r2。

固定两个圆的半径,改变 alph1和alpha2的值,看动态效果,第二个圆的圆周上的点a2,像月亮/卫星围绕地球/行星a1旋转,a1绕太阳即原点旋转。
1.5 轨迹
点击alpha1和alpha2右侧的 播放 按钮;

在a2的settings里面选择 show trace。

可以画出a2(以极坐标形式)划出的轨迹。

这个轨迹,模仿了托勒密的本轮-均轮系统,想像一下你站在原点,观测到的紫色线条就是某颗轨道令人困惑的行星在夜空里划下的轨迹。
1.6 函数曲线
在用傅里叶级数大轮套小轮画任意函数图像的过程中,我们在背景叠印一张函数图像作为参照,看起来更直观一些。
假设 alpha1 与 alpha2 有函数关系,例如
alpha2=alpha1*2。
![]()
叠印的函数,即大轮套小轮傅里叶级数在横坐标上的展开,如下。
![]()
任意时刻a2点在函数图像上的位置B,如下。
![]()
与a2纵坐标相同,画一条水平直线。在settings中设置为虚线,细一些。这条直线连接了卫星a2和在函数上的点B。
![]()
以上三项,函数图像、函数图像上的点、alph2与alpha1的函数关系 设置完毕以后,图像如下。

点击alpha1的播放按钮,观察以上图像的动作,可以注意到,(1)a2与B总在同一纵坐标,(2)B始终在紫色的函数曲线上。

2. 求两个参数 半径dk 和 初始相位差thetak
利用上一节中技术原型中涉及到的 geogebra 方法 画任意函数曲线的大轮套小轮傅里叶展开,我们还需要傅里叶级数的正弦形式。
根据 https://zhuanlan.zhihu.com/p/654224439 和 https://zhuanlan.zhihu.com/p/655415316
可以用Excel求得任意周期函数分解为傅里叶级数的 ak 和 bk.
又根据《信号与系统——使用MATLAB分析与实现》https://book.douban.com/subject/35627101/,有以下公式。

根据以上公式,可以由 ak 和 bk 求得 dk 和 θk。
其中dk为不同级数对应的圆的半径,θk为不同级数的初始相位角。
傅里叶级数表述为下述 正弦形式。

在Excel中,我们由上文中求得的 an 和 bn 求得 dk 和 θk。
在要拟合函数确定的前提下,傅里叶系数a1,a2……a5和b1,b2……b5已经求得。并且在Excel中傅里叶系数会随要拟合函数的变化而随时变化。
以d2为例,应用dk的公式,由b2和a2求得d2,得到下图。

以theta2为例,应用theta k公式,由b2和a2求得theta2。

这样,对于如下函数

可以得到d1~d5和theta1~theta5。
![]()
把d1~d5和theta1~theta5代入到上述傅里叶级数的正弦形式中,在Excel中就能得到下图中的右图。下图中的左图,是用an和bn即正弦和余弦均有的形式得到的,作为对比参考,它们完全相同。

(待续)
3. 画函数曲线
3.1 目标曲线
3.2 大轮套小轮-函数曲线横向展开
3.3 极坐标形式-原位轨迹跟踪