1. 问题
PQ同学在朋友圈提到，“如何理解一个数的无理数次幂？”我回复，“(3^x)^x = 9，求x。”
简单解读一下。写成更易读的形式为，在下面这个方程中求x。
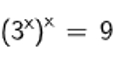
我们容易猜测到， 
刚好符合要求。接下来可能想到，解可能不唯一，然后想到 
也是一个解。所以，这个方程如果有解，那么要求3这个数的次幂是无理数。因此，如果这个方程有解、有意义、成立，那么，一个数（在这里是自然数3）的无理数次幂就需要有意义。换言之，这个方程就是一个数的无理数次幂的意义，就是“如何理解一个数的无理数次幂”。
以上对解的猜测是否正确，可以找一下旁证。
用Geogebra，没错。
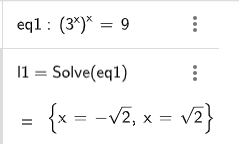
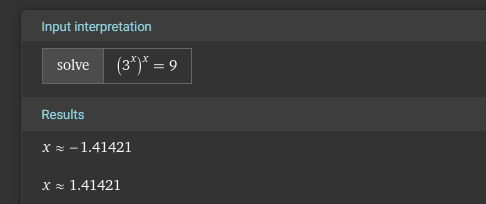
用 wolfram alpha https://www.wolframalpha.com/input?i=Solve+%283%5Ex%29%5Ex%3D9
得到2个解。
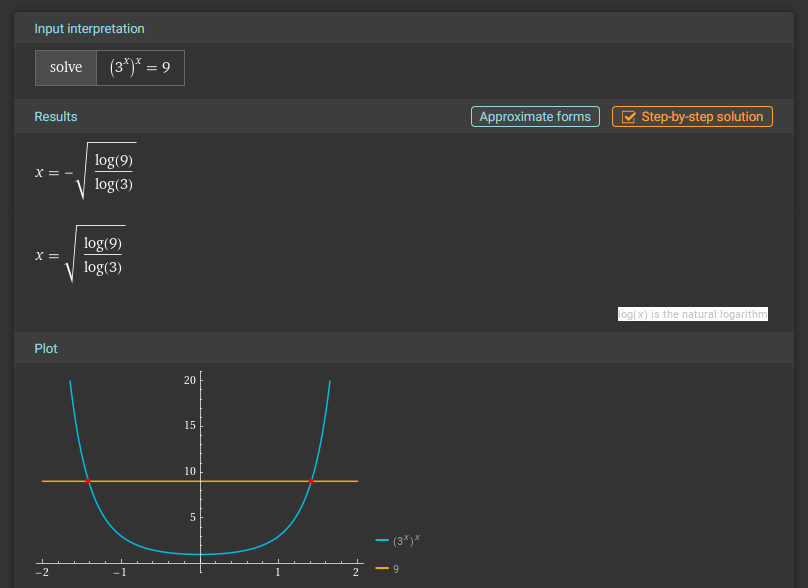
化简其中一个，结果没错。
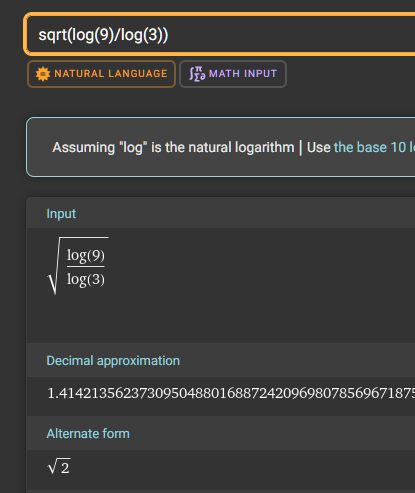
数值约等于1.414，正是我们熟悉的 +sqrt(2) 和 -sqrt(2)。
2. 对这个方程又如何理解
单单这么一个方程，看起来有点莫名其妙。你能会觉得这并没有回答，而只是对问题的重复。
这个方程类似在 数域扩展 和 数据类型 那一课中 所举的其他几个例子。我们略做回顾。
第一步 首先要有数。最初的数（似乎）是自然数。自然数是如何定义的？由0和+1操作可以定义出1。进而，由1和+1操作定义出2……这样，我们定义出自然数。
第二步 2+3=5，3+4=7。为方便起见，我们发现 自然数 可以用 加法 表示。
第三步 我们由加法定义出减法。7-4=3。5-3=2。7-4 的意思是 这样的一种运算——如果这个数x存在（有意义，有定义，有解）的话，方程7-4=x有解，即 x+4=7，也就是说那个数是 加上4等于7的那个数。当然，后来我们知道这个数刚好存在，并且唯一，是3。
根据减法的定义，我们列出式子 2-3。根据定义，其含义为 2-3=x,即x+3=2，加上3等于2的那个数——如果这个数存在的话。这个数不存在，在所有自然数中，当我们遍历时可以发现，没有一个数加上3能等于2。
第四步 为了2-3=x或x+3=2这个方程有解，我们扩展数域，令x=-1。我们把这个新的数域，也包括旧有的自然数，起个名字，称为整数。
负数或者说自然数以外的整数为什么存在？如何整理负数？负数，就是令2-3=x有解的那种数。如果想解这种方程，那么就需要负数。如果某个物理现象的建模所得到的方程，即各种变量间的约束关系，刚好就是这样的方程，那么我们就需要负数。
书说简短，我们按这样的方式，即因为方程需要有解（因为运算或逆运算是有定义的，因此应该可解），继续扩展数域，就得到了分数/有理数、实数中的无理数、复数。
回到最初的方程上来。这个方程(3^x)^x = 9看着如此简单，不应该无数吧。如果它有解，我们就必须接受次幂是无理数的，否则方程无解。
3. 如何构出这个方程
构造这个方程不是“显然”就写出来了。
看问题 “如何理解一个数的无理数次幂”时，我首先想到 有什么情况下会有无理数次幂。
所以，我需要一个方程。类似这样的方程 一个数^(x)=另一个数，即一个数的无理数次幂的值是另一个数。2^sqrt(2)=管它什么呢，这就是无理数次幂。但这是没有意义的，是对问题的重复。
什么是有意义呢，我们在什么情况下需要次幂是无理数？答案是：这类同于数域的扩展。
我需要类似 2个数的平方等于2 的形式，这样其解就是sqrt(2)，无理数。那么我需要 x*x 的形式。加法不行，减法不行，一定要乘法才行，sqrt(2)就是那个 自乘等于2的数，x*x=2 的那个x。
3^(x*x)=9，这就有意义了。这个方程不需要 问题中的无理数次幂 就可以定义出来。并且，这个方程易懂，我们能猜出来它的根有sqrt(2)。
但是还差一点。这个方程确实没有引用未定义的概念无理数次幂，但是它的解是2，也没有引出无理数次幂（必然存在）这一结论。
变换一下，3^(x*x)=(3^x)^x，这样就可以了。这个公式叫做什么来着？
这样，我们就得到了 (3^x)^x=9，其解是无理数的次幂。
3. 物理意义及扩展
这个方程(3^x)^x=9在数学有意义了，但是有的同学可能还会追问，这样的方程有必要存在吗？那么，所追问的就是这一类方程，或者说无数数次幂，的物理意义。
物理中有没有这样的方程呢，我首先想到的是欧拉公式，那是复数次幂。实数的，还非得是无理数的，有理数/分数的不行，一时没想起来。搜索了一下。我才知道无理数次幂是高中数学的内容/捂脸。
又搜到
为什么几乎所有的物理公式里面的参数都是有理次方的？ - Boo Radley的回答 - 知乎
https://www.zhihu.com/question/418475291/answer/2120030068
有回答指出 半衰期、热力学中的多方过程 都可能是无理数次幂。
突然想到前几天刚刚又看到的，维度。相当于下面这个回答中的，维度有一维、二维、三维，还有分数维度，还有无理数维度。正是按数域扩展的思路，“如果符合定义，我们还可以得到这样的结果；它有点匪夷所思，但是符合定义”。
在物理中，是否存在某个物理量正比于另一个物理量的无理数次幂的情况？ - 笠道梓的回答 - 知乎
https://www.zhihu.com/question/396816857/answer/1242606325
接下来，我们可以按同一思路继续讨论。一阶导数是什么意思，二阶导数是什么意思，都是有定义的。那么，1/2导数是什么意思，sqrt(2)阶导数呢？
https://www.zhihu.com/people/yang-gui-fu-52
