对于实现需求“一副哑铃,有可替换的哑铃片 0.75kg,1.25kg,2kg,2.5kg每种各4片。可以组合出哪些重量”,此前写过一篇博客,https://zhuanlan.zhihu.com/p/702387535。我当时感觉有条件的穷举相当困难,束手无策,二猫用C/C++解决了。上次那个故事告诉我们,精确描述需求经常相当困难,即使你觉得问题简单并且考虑清楚了。
前两天练着的时候,突然想到,好像用Excel能解决。这次的故事告诉我们,如果需求清晰了,一切都不是问题。
总体的思路是——先穷举、再过滤。
问题1. 约束条件:两个哑铃重量相同,每个哑铃的两端重量相同。
2.5kg,2kg,1.25kg,0.75kg 共4种哑铃片。
思路是这样的。
(1)在每个重量组合中,4个哑铃片的每个有2种状态,
分别为0和1,1代表取、哑铃片拧在杆上,0代表舍、哑铃片不拧在杆上。
(2)哑铃片彼此重量不同,因此分配4种不同的权重,对应二进制每位2^3~2^0。
步骤如下。
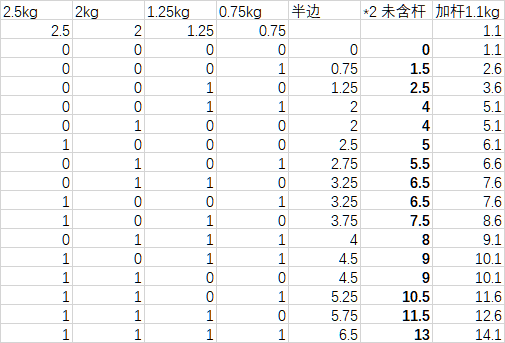
(1)Excel表格的左半边,函数的自变量及取值。
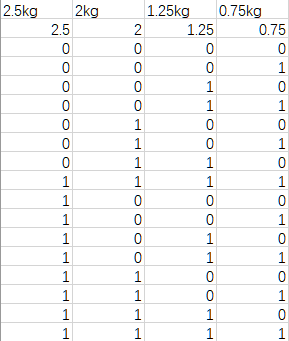
第1行以4种哑铃片的重量作为标签;
第2行的数据是哑铃片的重量,用于接下来的计算。
第3行开始穷举4种哑铃片的所有状态可能。
其中 0000代表4个哑铃片都舍;
0001中的1代表0.75kg哑铃片取,其余哑铃片舍;
0010中的1代表1.25kg哑铃片取,其余哑铃片舍;
0011代表1.25kg和0.75kg哑铃片取,其余哑铃片舍……
其2^4=16种可能。
(2)Excel表格的右半边,函数值。
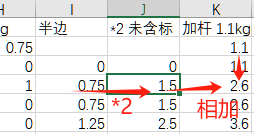
“半边”这一列,用于计算单个哑铃一端的重量。公式为
每个哑铃片的重量 * 每个哑铃片的状态0或者1 ,4个哑铃片累加。
也即 sigma( 每个哑铃片的重量 * 每个哑铃片的状态 )
也即 2.5kg*状态a + 2kg*状态b + 1.25kg*状态c + 0.75kg*状态d
下图中,D6是0.75kg哑铃片的状态,d是0.75kg哑铃片的重量。
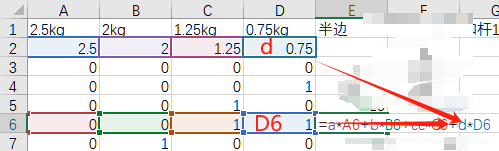
如下图,得到哑铃组合的16种可能。
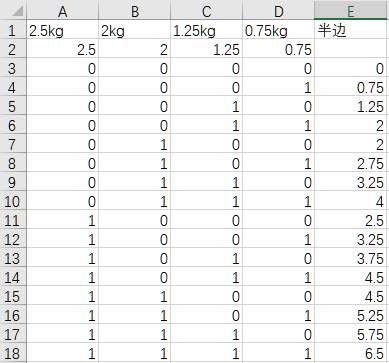
(3)接下来,把单个哑铃的一端加倍,再加上杆的重量1.1kg。
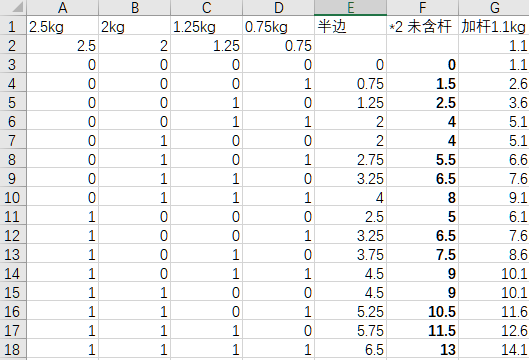
16种可能,不重不漏。其中有些组合的重量是相同的,给予保留。在锻炼中,这时的重量分布不同,旋转等动作的时候会有不同感觉。
按重量排序。需要排序的原因分析在第2个问题中详述,此处从略。
问题 2. 放宽的限制条件:只组装出单个哑铃。
限制条件:每个哑铃的两端重量相同;每端不超过4个哑铃片。
2.5kg,2kg,1.25kg,0.75kg 共4种哑铃片,每种2片,共8个。
(1)自变量-取舍状态,穷举所有可能,函数值-哑铃重量。
下图为局部,只包括了所有可能中的8种。
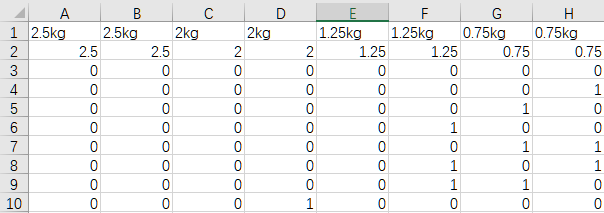
按问题1中的思路,把每片哑铃赋值为一个自变量,取值为拧上或不拧上的状态1或0。共2^8=256种可能。
函数值,半边(单个哑铃的一端)重量,取值为
Sigma( 每个哑铃重量 * 每个哑铃片的取舍状态)
下图为局部,只包括了所有可能中的4种。

接下来,求单个哑铃的两端,再加上杆的重量。
(2)过滤条件1 相同重量哑铃片的去重
有一种情况,在穷举中认为两种不同组合,但在需求中视为相同的组合,需要去重。
例如:两个0.75kg哑铃片间没有任何不同,因此取任何一个,在需求中认为相同。但是在上述穷举中两个0.75kg哑铃片的状态是不同的变量,所以未去重。
解决方案如下。
两个相同重量的哑铃片,设1为取,0为舍,共有如下4种可能组合。
| 哑铃片a | 哑铃片b |
| 0 | 0 |
| 0 | 1 |
| 1 | 0 |
| 1 | 1 |
我们可以注意到,以上4种组合中 01 和 10 两种状态是完全相同的,因为在需求中两个相同重量的哑铃片没有任何不同,二者取哪个并无区别。
根据以上分析,我们过滤掉 10 的这种情况。
即 遍历4种哑铃片,只要其中任何一种哑铃片有10这样的组合,去除这一组合。
在Excel中分两步完成。
第一步 取重量相同的2片哑铃,如果组合为10,作标记为1。
算法是 左侧的权重为2^1=2,右侧的权重为2^0=1;如果 左*2 + 右 的值 为2,那么标记赋值为1,否则赋值为0。如下图所示,标记“0.75kg - 10”为1。

第二步 遍历所有4种哑铃片,作 或操作,即4种哑铃中有任何一个符合(组合为10),对“有哑铃片存在10组合”标记为1。如下图所示。其中的“+0”是为了把TRUE或FALSE转为1或0的形式。
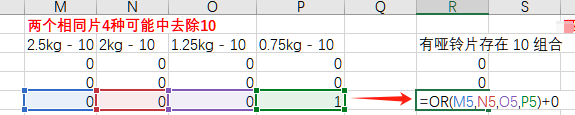
(3)过滤条件2 哑铃片超过4个,去除
对左侧的状态 求和,哑铃片每取1片会有加1。如果总数大于等于5,对“哑铃片4个及以下”作标记1。

(4)过滤条件1 + 过滤条件2
上述两个条件中任意一个标记为1,那么标记“两条件过滤”当前组合为1。

设置筛选条件如下,去除所有标记为1的行。
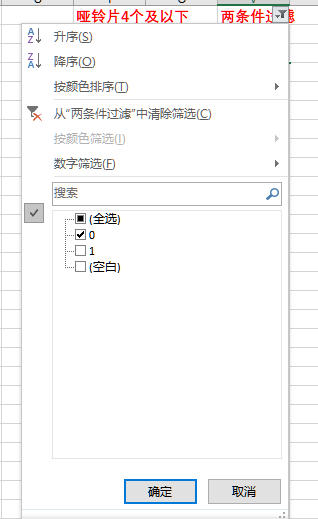
(5)排序
筛选完成后发现,与问题1不同的,哑铃的重量并非由小到大升序排列。原因是二进制权重(以及所有带权的进位制)都假设 右边的所有位取1所得到的结果,小于 左侧任意一位的值。如二进制的100 > 011,如十进制的 1000 > 999。这样,按0000~1111穷举权重,得到的结果才是符合升序排列的。即相当于按下图的条件排序。
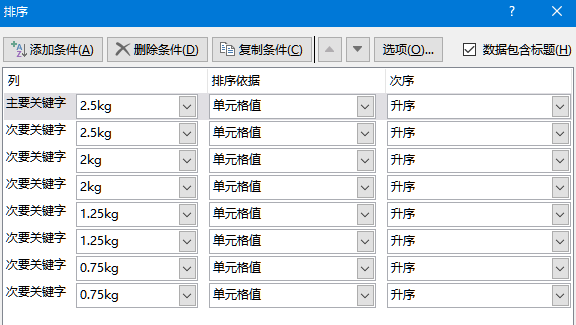
在下述反例中,
状态0000 1111得到重量4,
状态0001 0000 得到重量2。

状态 自变量值 0000 1111 < 0001 0000,
重量 函数的值 4 > 2。
这导致的按状态升序排列所有组合,函数值并非全都符合升序排列。
在Excel中,容易处理,按列 半边重量(或*2未含标,或加杆1.1kg,顺序相同)排序。
或
(6)得到结果
因为有筛选,所以如果想把结果复制粘贴到Excel之外,会把筛选掉的组合也一并复制粘贴出来。
排除筛选掉的行的方法,在Excel中按如下步骤操作。
第一步 Ctrl-g 或 F5 得到 定位对话框。
选择 定位条件。在下图中选中 可见单元格。
Ctrl-c复制,打开或新建 另一个工作表,鼠标右键 | 选择性粘贴。如下图所示,按 数值 粘贴。
共49种可能。经与二猫的工作核对,一致,旁证我的结果是对的。
画图分析,双哑铃 其中每个哑铃重量的增长,如下图所示。
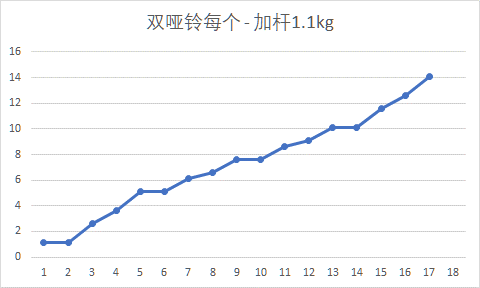
从图中可以看出,(1)增长较为平缓,这样锻炼时可以组合出步进不那么激进的重量;(2)某些重量有不止一种组合。相邻求差发现步长有三种,分别是0、0.5、1、1.5。其中6处步长为1,4处步长为1.5,2处步长为0.5.
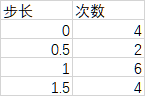
单哑铃的重量增长,如下图所示。具有与双哑铃相同的特性。
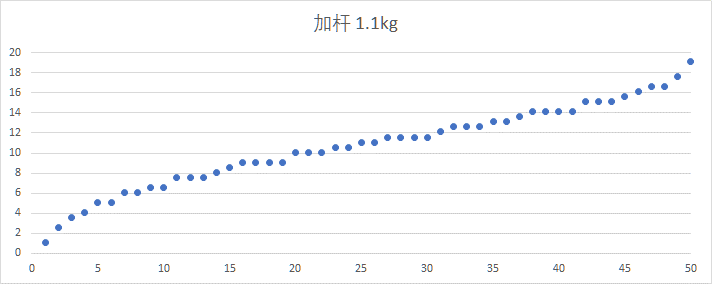
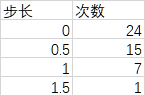
相邻求差发现步长有四种,分别是0、0.5、1、1.5,其中多数是0.5,更多哑铃片使增长更平滑。7处步长为1,1处步长为1.5——最后一步。
-----
https://zhuanlan.zhihu.com/p/709971919
微信公众号:杨贵福
