1. 问题
十进制小数转为二进制小数点以后的部分,课本中的方法,是“乘2取整数”。做乘法次数相当多,直到小数部分为0,或者达到要求保留的位数。手算容易出错。
Excel和Windows内置的计算器都不支持小数部分由十进制转换为二进制。
本文提到的方法是从 https://www.instructables.com/Convert-Fractional-Decimal-to-Binary-Using-Calcula/ Convert Fractional Decimal to Binary Using Calculator!!! 学来的,适合十进制小数转换为二进制时的手动计算。用这个方法,也可以非常方便地用Excel或计算器辅助完成。
2. 方法
方法的步骤和基本原理如下。
要转换的数,我们称为d;
转换后要保留的二进制位数,我们称为p。
例如,我们要把 1.732转换为二进制,二进制小数点后保留7位。
这样 d=1.732,p=7
第1步 d * 2^p,在十进制内操作。
即 1.732*2^7 = 221.696
计算器支持这一计算。
手动计算的话如下式。因为在十进制内计算,所以比乘二除整的步骤要少,不那么容易出错。
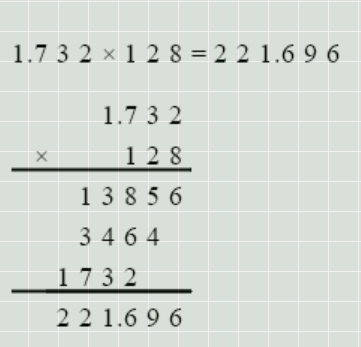
上式用[http://www.xushanxiang.com/tools/mvg/]生成。
第2步 把上一步结果中的整数部分转换为二进制。
221转换为二进制为11011101。
计算器支持这一计算。或者除计算器外,这一计算也可以用除2取余法手动完成。或者这种较小的数可以逐次减去2的整数次幂求得,如下表。
| 2^7 | 2^6 | 2^5 | 2^4 | 2^3 | 2^2 | 2^1 | 2^0 |
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| If(221>128) | If(221-128)>64 | If(221-128-64)>32 | … | … | … | … | … |
| 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
第三步 把上一步结果的二进制除以2^p,在二进制内进行。
11011101除以2^7。在二进制中,每位权重为2,因此除以2^7,即小数点左移7位。
类似十进制中除以10^3,即小数点向左移3位。
1 1 0 1 1 1 0 1 向左移7位,如下图。
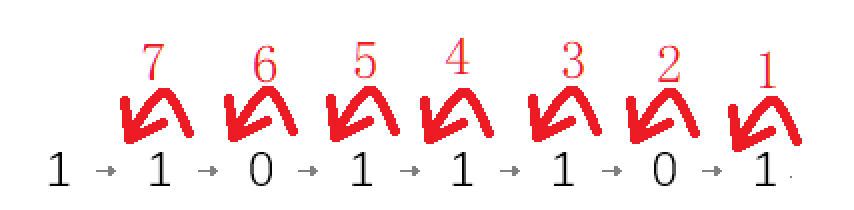
得到1.1011101。
第3步的结果,就是要求的二进制数。
结果正确的原因是,第一步乘以2^p,第三步除以2^p,所以结果不变。
能够使用计算器的原理是,第一步乘以2^p,可以把所有将转换为小数的部分都变成整数,整数就可以用计算器来辅助了。
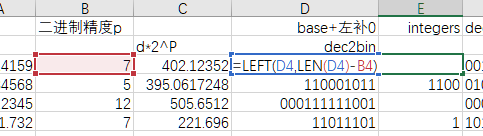
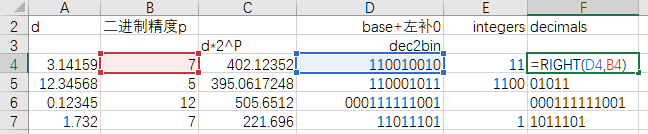
3. 用Excel实现
用这一方法制作Excle如下。
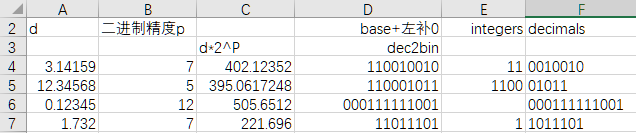
其中列A和列B,分别是要转换的数字十进制小数d和二进制的精度p。
列C对应上述步骤中的第1步,在十进制内乘以2^p。公式如下。

列D对应上述步骤中的第2步,按列B的精度把列C转换为二进制数。
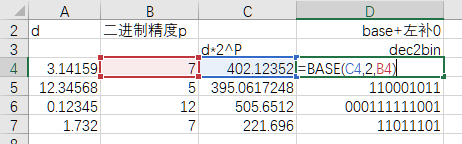
拆分列D,分别得到整数部分列E和小数部分列F。公式如下。
4. 未尽事项
上述步骤中对小数部分做舍去处理,未讨论舍入,需要单独另行考虑。
