1. 虚数i开平方根
二猫问,-1开平方根,得到的是虚数i;虚数数i开平方根,得到的是什么呢?
即 已知sqrt(-1) => i,
问 sqrt(i) => ?
2. 不能开方-什么是开方
简单粗暴的回答是,i不能开方。这种回答也不是没有先例,在除法里,我们规定 任何数都不能除以0。就这么规定的,似乎也没有什么原因。
真的没有原因。有,老师十有八九也讲过,可能咱们都没有注意到,或者后来考试也不是重点,咱们就忘了。就像网上公众号提到“吾生也有涯,而知也无涯”后面还有半句,不少人大呼被课本骗了。语文课本的书下注释明确写了后半句,“以有涯随无涯,殆已(我印象里是 汲汲乎怠哉。存疑”。这样的例子还有,共同点是你自己没注意怨谁。
a/0 非法,原因是 任何数乘以0都不能等于a。这是当时老师讲的。其背后的原理是 a/
0 并非一个数字,甚至这个数是否存在我们都不知道。a/0不是个数字,它是个运算。a/0表示这样的运算,如果这个运算可以求解,那么得到的数字 乘以0等于a。
类似的2/3的意思是 这是个运算,这个运算如果可以求解,那么所得的数字是 乘以3等于2的那个(那些?)数字。为了表示2/3这样的数字(!)我们由整数域扩展得到有理数域,这是另一个故事,按下不表。
我们确实有过规定,规定任何数不能除以0。那么是否有规定 i不能开方呢?不记得。
那么,我们类推一下。除以0的先例中的规定,要看除法的定义。虚数i是否能开方,我们要看看开方的定义。
什么是开方?
开方是一种运算,sqrt(a)的意思是 如果这个运算可以求解,那么所得的数字是 平方以后等于a的那个(那些?)数字。
运算sqrt(-1),得到的结果是i。为什么呢,因为 i^2 即 i*i => -1。这是开方的定义决定的。
那么sqrt(i)的意思是什么呢?这有点麻烦,我们暂且搁置这个话题,用geogebra求一下。
3. 用geogebra试试
先测个空白,sqrt这个函数能不能用。

这什么玩意。

世界上第一个无理数,这个可以。
看来geogebra可能有特殊的语法,我不会。想个诡计吧。

-1的平方根是i,这是已知部分。

可以,可以。虚数i的平方根是0.71+0.71i,一个复数。而且geogebra贴心地给出了这个数在复平面中的位置。

图中,z1是虚数i,z2是sqrt(i)。
我说,看起来z2也能求平方根啊。二猫说,肯定能啊,既然它也是个复数。
我在geogebra里输入z2,怎么也不对。二猫说,“得用 z 下划线 2”吧。我心想,你平时偷摸学了不少啊。
结果是这样的。

4. 复平面-乘法的含义-手动求sqrt(i)
我若有所思,0.71……这数字咋这么熟悉呢。
过了一会儿,我在白板上画了下面这张图。
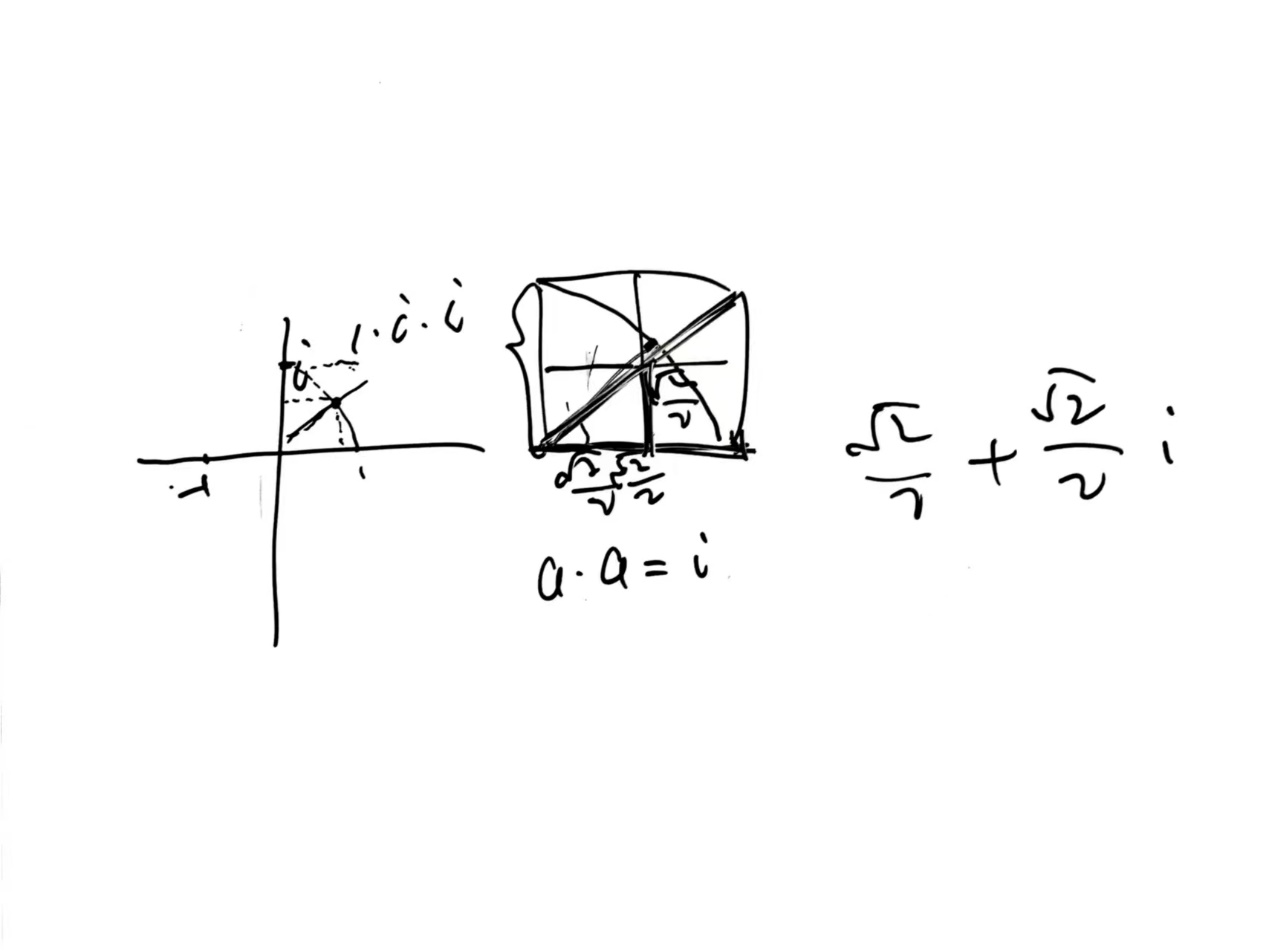
回到刚才我们暂时搁置的线索——开方到底什么意思。
开方是这样的运算,如果a=sqrt(x),那么a是这样的数字a*a=x。一个数字x开方得到的数字a,a自己乘以a自己,能得到x。
那么sqrt(i)什么意思?一个数字,这个数字自己乘以自己,其结果是虚数i。
下一个问题,什么是乘法?在复平面上,我们已知(什么时候知道的?我也不知道,反正应该已经知道了)乘法是 绕原点逆时钟旋转(我们姑且忽略模的增长,假装没这回事)。
小结一下,
开方 是……符合……的乘法。
乘法 是 绕原点逆时钟逆转。
虚数i是什么?复平面上 坐标为 (0,1) 的那个点,即z1。

虚数i开方,就是 有个数字,它旋转两次相同的角度,就能从x轴正方向到达 (0,1)。这个数字是什么?
虚数i是(长度为1)角度90度的那个点。哪个点旋转两次相同的角度能达到90度?45度。
所以,虚数i开方,是长度为1,角度45度 的那个点。
长度为1,角度45度 的那个点的坐标是什么?在单位圆里,那个点的横坐标是 半径1*cos(45),那个点的纵坐标是 半径1*sin(45)度。
三角函数 sin(45)=cos(45)=sqrt(2)/2,即

结论,sqrt(i) => 0.71+0.71i.
这一结果验证了geogebra的sqrt的结果。
5. 任意复数开任意(实数)次方-十二平均律
我们可以再求得更具有一般性一些。
虚数i的3次方根,结果是多少?那个斜体(?)的i是按alt+i打出来的。


-1 的2/3次方根,结果是什么?


数字长得像而且眼熟?因为那是60度和30度的正弦和余弦。是对180度和90度三等分得到的角度。
几次方根,就是把角度等分多少份。因为几次方,就是自乘/旋转几次。所以几次方根就是几等分角。
十二平均律,就是把一个八度内的音程等分成12分。跨八度是频率乘以2,所以等分就是开12次方根。
2/3方根就是三等分,再取两份。
十二平均律中一个八度里的第2个音,距离最左面3个8度^1/12,即3个倍频的12次方根,就是对倍频12等分,再取2份。
6. 数域
听说,复数是数域扩展的终点。所有的运算,其来源和结果一定不会超过复数的范围。
如上示例,任意复数可以开任意实数的方根。那么,任意复数,可以方根时,可以开任意复数的方根吗?
虚数i的虚数i次方,即i^i,如下图所示,这样行不行?
![]()
复平面上的几何意义是什么?需要扩展数域才能计算?

复数是数域扩展的终点吗?
