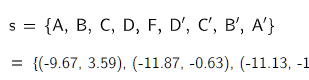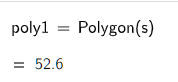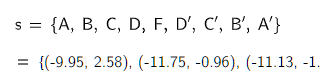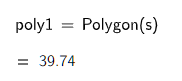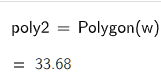1. 目的
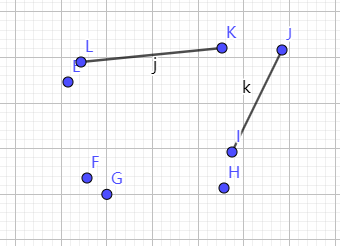
看机械入门的书里提到,船只侧倾时会自动回车的原则,是因为船受到的浮力在船重心的旁边,像个杠杆,形成的力矩会推动船只恢复到竖直的角度。还配了一张图,看起来就像作者说的那样。真是这样吗?
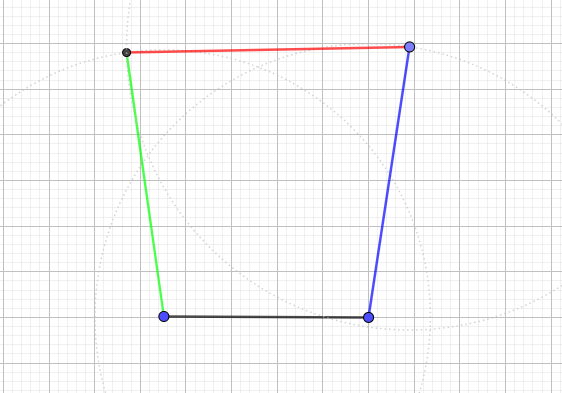
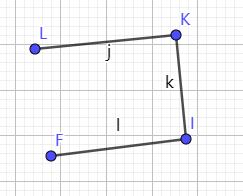
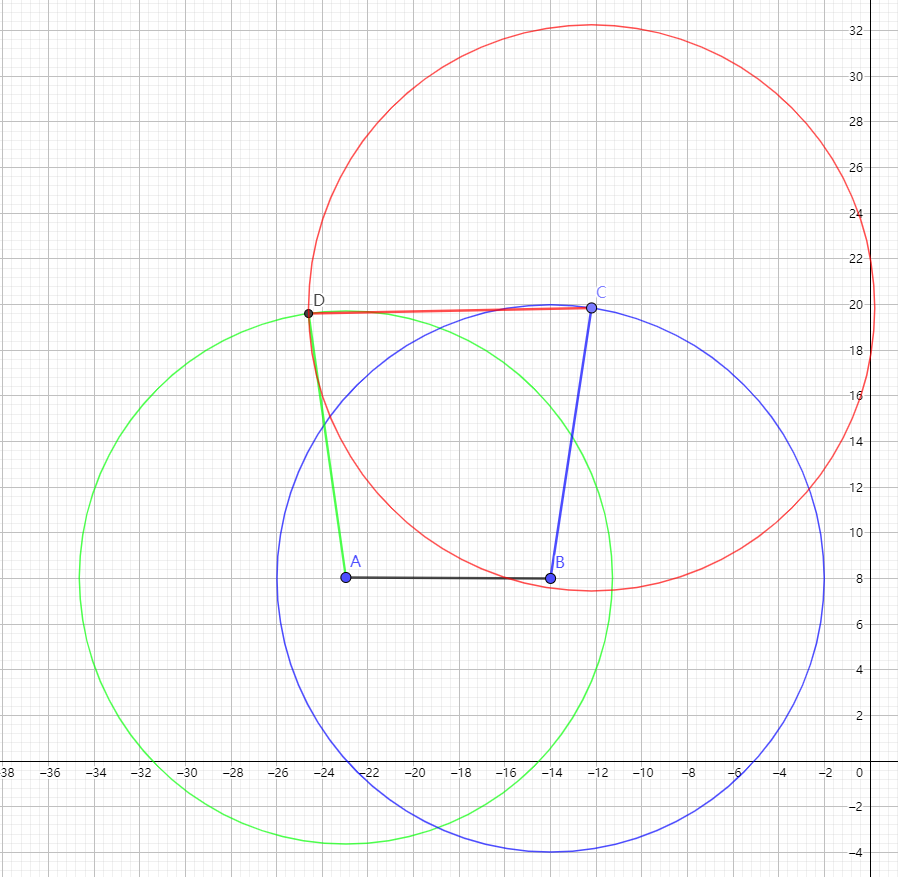
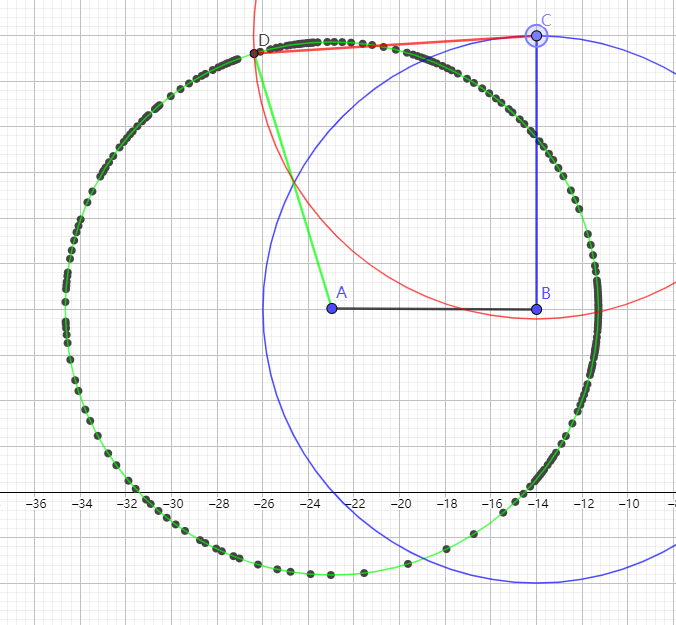
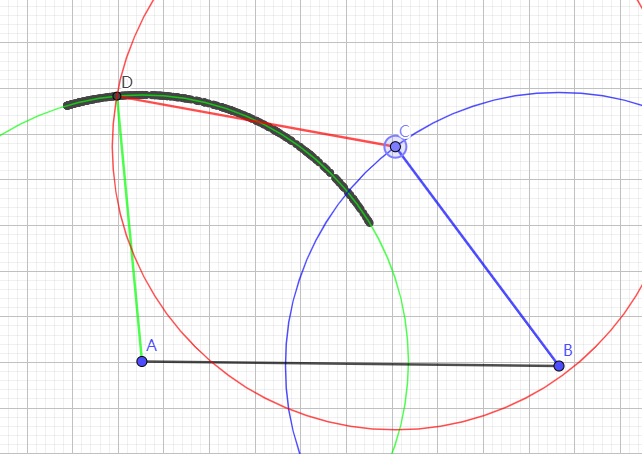
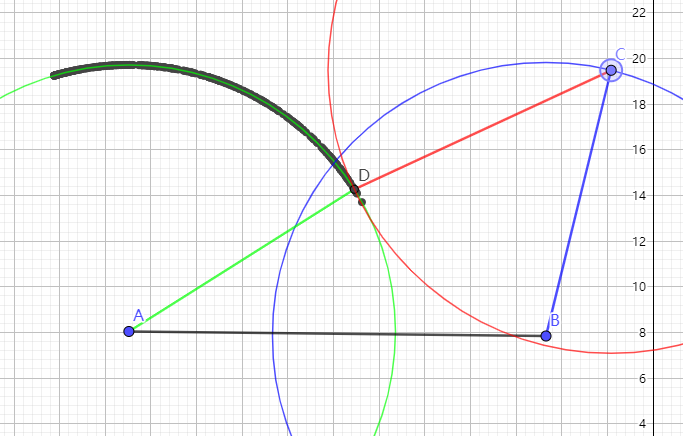
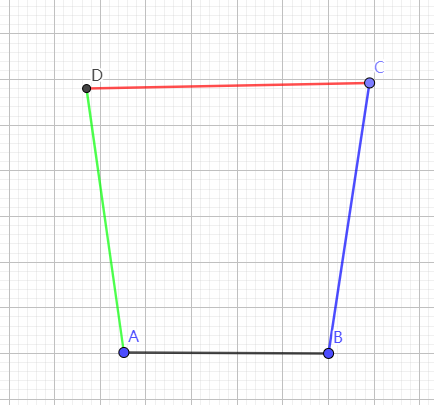
书上的图大致如下图所示,图是我用geogebra画的。
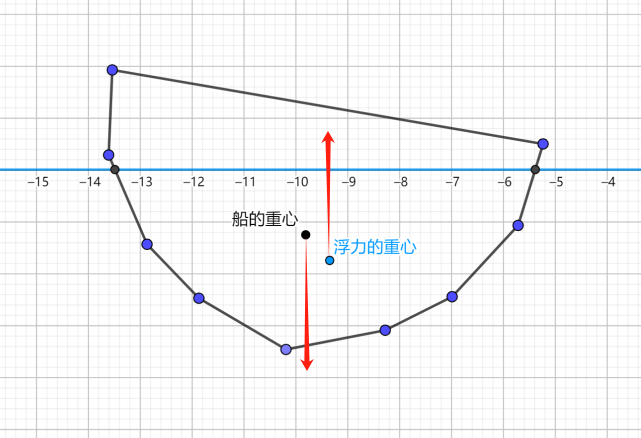
科学的特点是每个人都可以做实验证伪,如果有一次实验失败了(且不能解释),那么假说就是假的。如果没有实验条件,我们也可以在纸上推导,只要内部有一处矛盾,那么假说还是假的。有geogebra,我可以自己试试,很方便。
2. 技术原型
2.1 这一节是错的,承蒙李腾飞老师指出
我要做的包括(1)画船的剖面,从正前方向后看,计算船的重点;(2)水平线,计算船在水下部分的重心,即把船视为质点时的浮力,称为浮心。把两条放在一起考虑,我需要的技术原型是 求多边形的重心。
以下保留错误作为引文。
-----错误引文开始-------
在 https://glamas.github.io/geogebra_commands.html 查到求重心的函数,英文版是 Barycenter,中文版是 重心。手册在这里 https://geogebra.github.io/docs/manual/en/commands/Barycenter/。
Barycenter( <List of Points>, <List of Weights> )
Geogebra给出的例子如下。

第一个大括号里是多边形的所有点;第二个大括号里是每个点的权重,这里我假设船体是均质的,权重都是1。
试一下。随便画几个点,求重心。

得到的图如下。
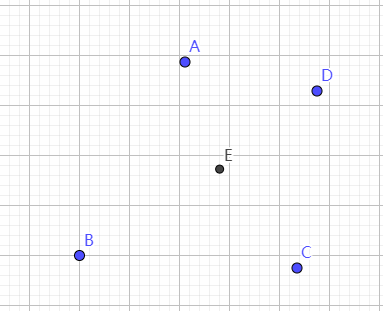
E就是求得的重点,位置看起来挺像重心的。
随便拖动一个点,例如A,换个位置。重心随之移动。
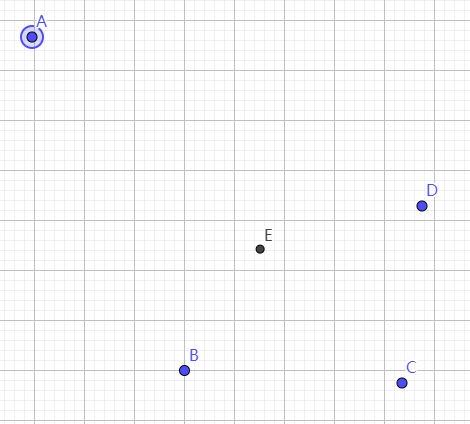
进一步验证重心是对的。
------错误引文结束-------
2.2 正确的做法
我望文生义,以为 barycenter 就是重心。
但是李腾飞老师说,你得看手册啊,“仅仅就是对点到列表加权求均值”。大意如此,不是原文。这正是我常跟同学们讨论时用的那句,RTFM。
手册在 https://geogebra.github.io/docs/manual/en/commands/Barycenter/,原文是“defined as the average of their positions”。加权平均,不是重心?
李腾飞老师说,“杨老师你想,如果我在一个对称图形的任意一侧边上加一个点,明显重心不变。但输到这个函数里,明显值就变了”。这反驳太有力量,以至于我哑口无言。如下图,在P,Q,R,S这个多边形非常靠近的地方加个点T,(物理意义上的)重心明显不变,但是barycenter这个函数的值,即加权平均,一定变了!
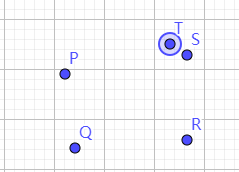
Barycenter,并不是我们需求的物理重心。
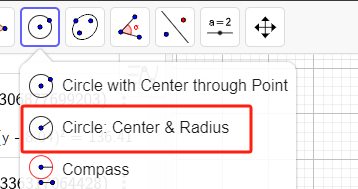
那么,重心用什么求呢?李腾飞老师告诉我,“用geogebra内置形心函数Centroid(Polygon(顶点坐标列表))可求的质心即重心。”
用法如下图中的示例,得到的点N即形心,也即物理的重心。
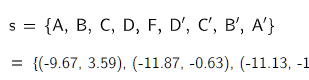
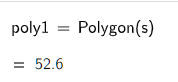

3. 步骤
那么开始做船吧。
第1步 画半边船
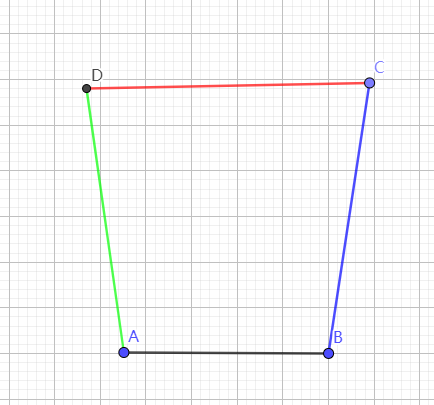
从前方向后看,画出船的剖面。为方便后续步骤起见,船不是竖直的,而是侧倾的。
随便4个点,看起来像船的半边即可,坐标不重要,所在在此省略。
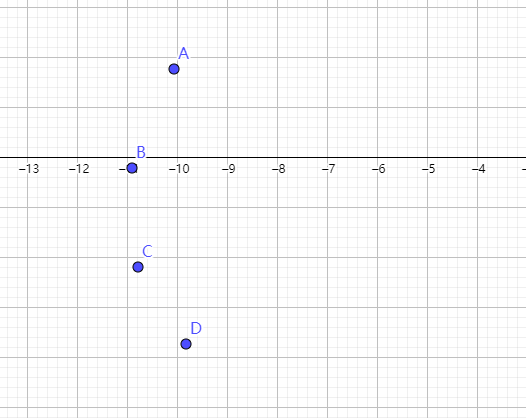
第2步 关于船的中心线对称,得到船体剖面
画一条斜线,就是船的中心线。
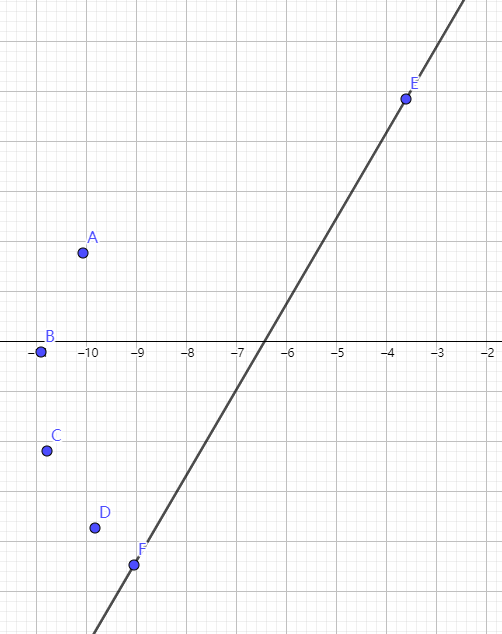
做对称。选中船剖面的4个点A,B,C,D,对于直线EF做对称/反射。
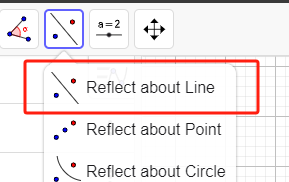
得到下图。
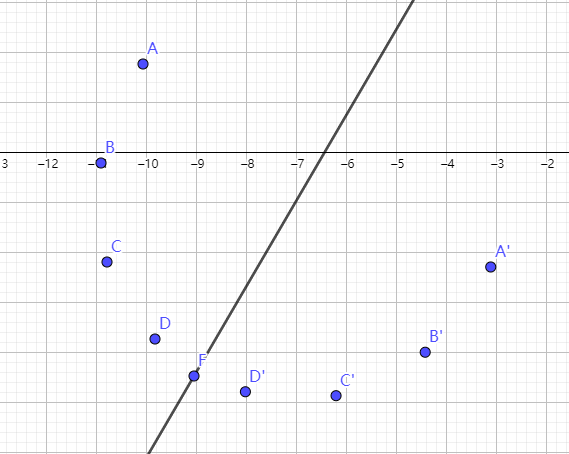
连接所有点,构成船体的剖面。
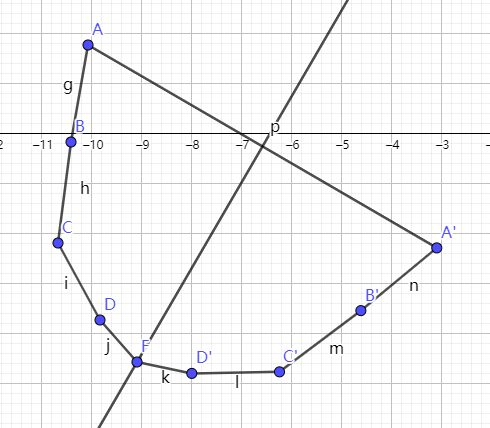
第3步 求船体的重心
指令如下。前一版本错用了 barycenter函数,这一版已按李腾飞老师的指点修改过。
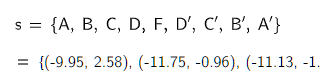
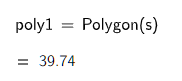
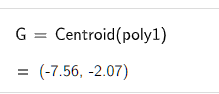
画出重心如图所示,其中点G就是重心。
随便改变几个点的位置,重点G随之改变。
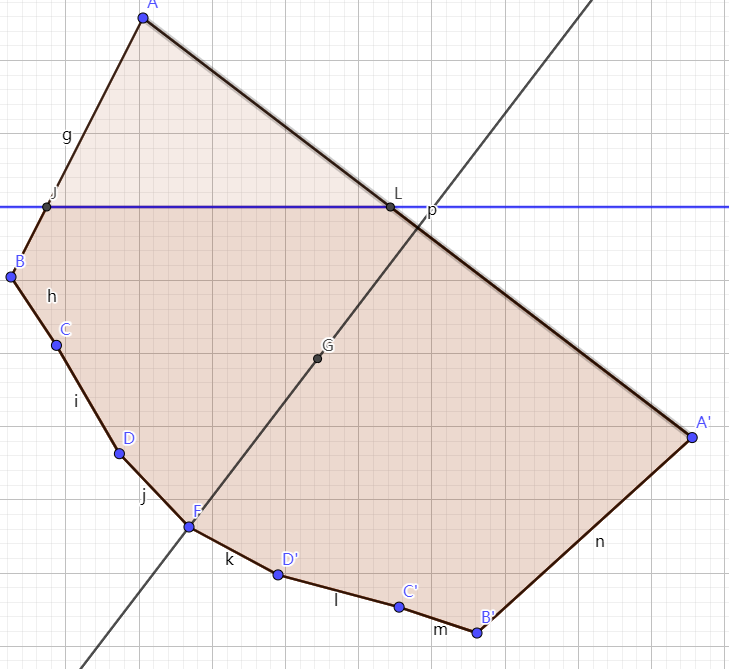
A,B,C,D,F点可以主动改变,A’,B’,C’,D’不可以主动改变,只能被动由直线EF对称得到。
第4步 求船受到的浮力,即船体排开水的重心
根据阿基米德浮力定律,船体受到的浮力即排开船体排开水体的重心。
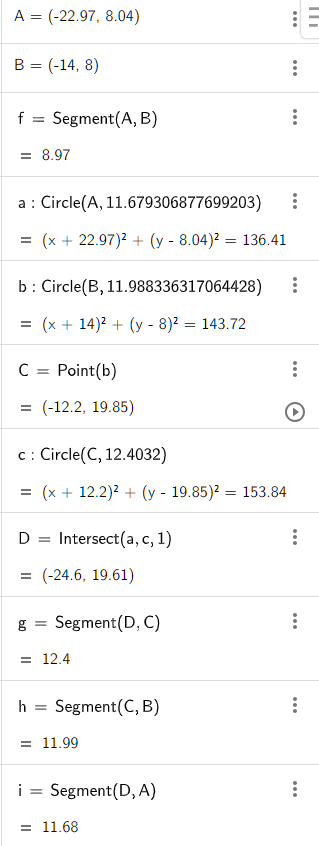
画水平面,求得水平面与船的交点。
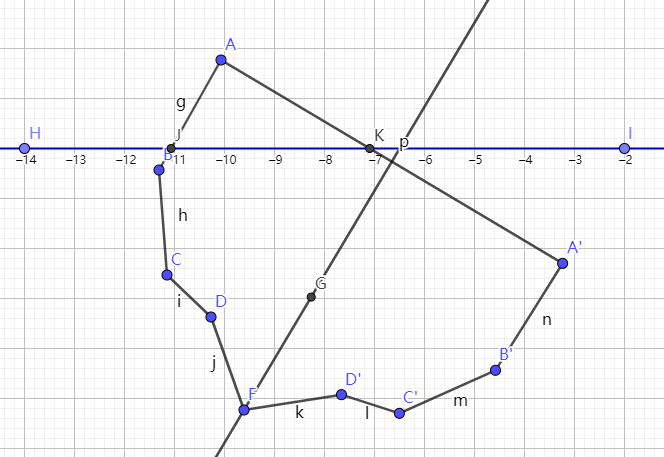
蓝色直线HI代表水平面,与船体的交点是点J和点K。
求船排开的水体的重点,即 J,B,C,DF,D’,C’,B’,A’,A,K 的重心。前一版本错用了 barycenter函数,这一版已按李腾飞老师的指点修改过。此处有另一错误也蒙李腾飞老师指出,他告诉我“还有在帖子的第一种情况中,求排开水的形心的多边形时,误把A点包含进去,应以J点收尾”。这一版本已修正。

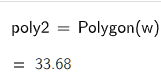

得到下图。
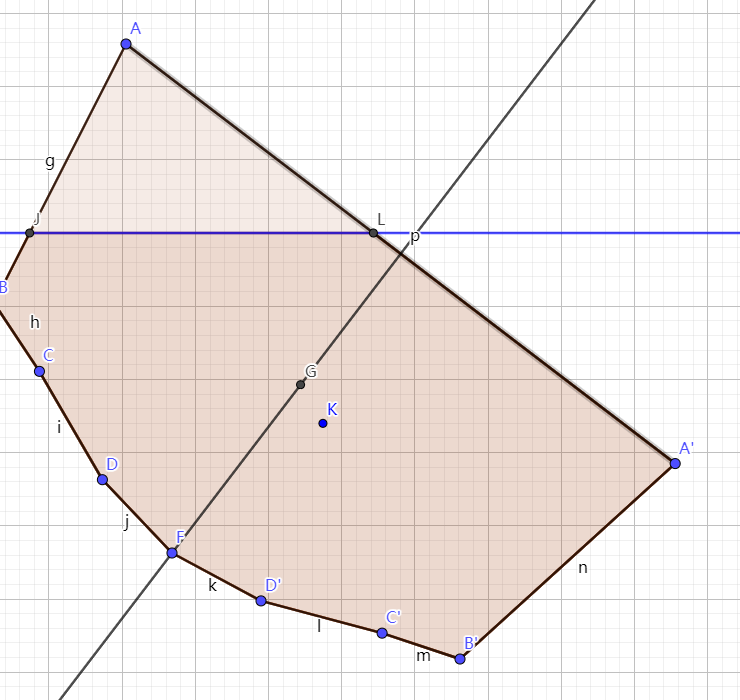
在上一版本中,由于(1)用错了求质心的函数,(2)点的序列错了,所以“浮心在重心的左边,这会继续侧倾,然后船就沉了!”如下图所示,接下来还做了讨论,以下作为引文。
----错误引文开始-----------
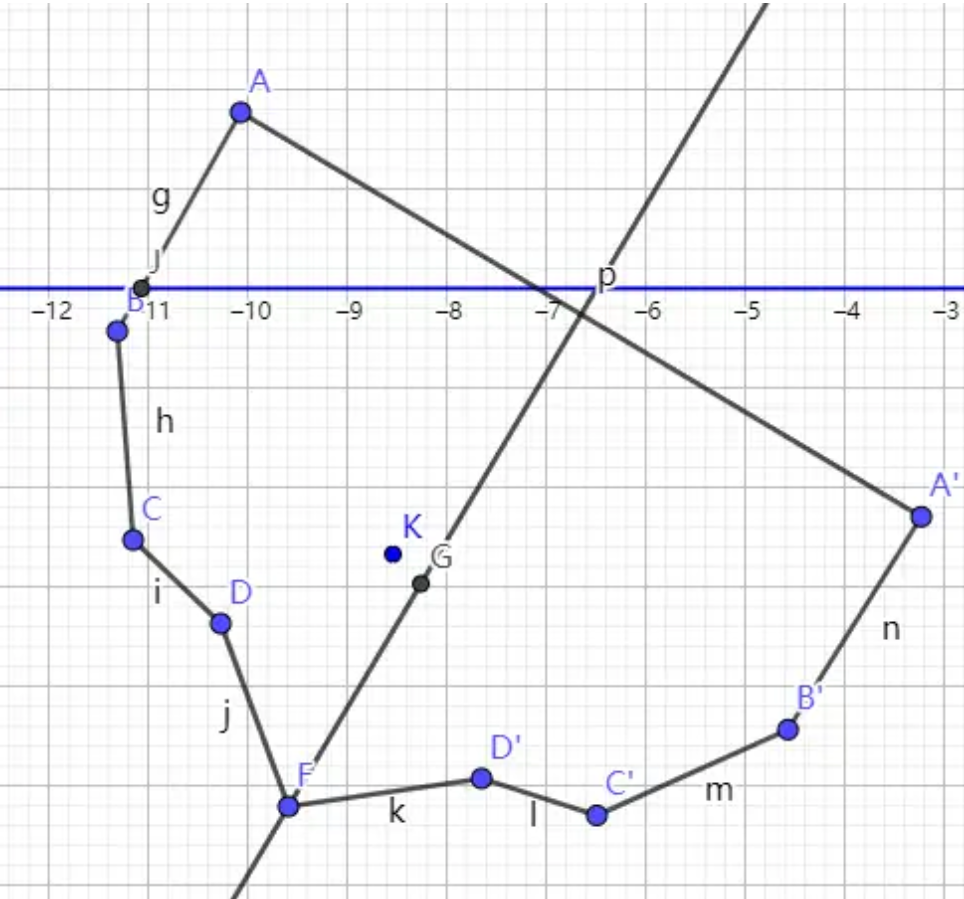
通过剖面上的点和对称轴,调整一下船的截图,再求一次船体与水平面的交点,再求重心。

这回看起来对了。
----错误引文结束-----------
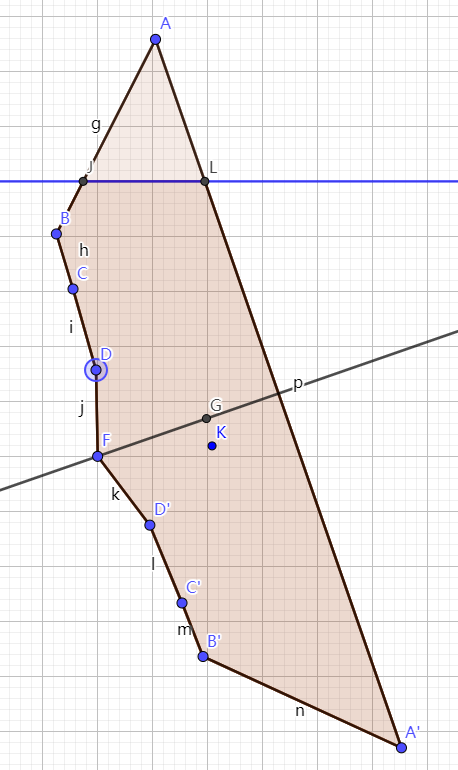
根据李腾飞老师指出的,用形心函数、点的序列保证正确,当船体右倾时,浮心总在重心的右侧,形成的浮力矩总是倾向使船体回复竖直。并不存在我担心的侧翻情况。
即使侧倾至对称轴水平,船体旋转90度,回复力矩仍然存在。
4. 随便改改
随便改改参数,有利于提高我们对问题的感性认识——以及更重要的,提高成就感。
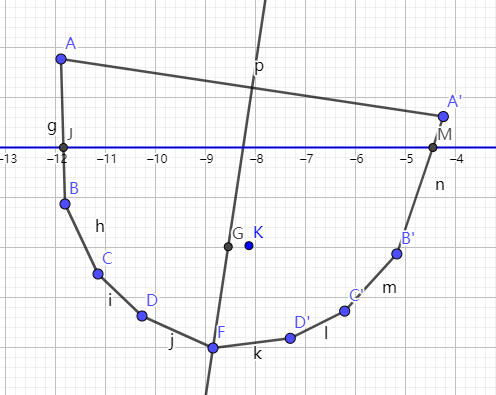
随便改变一下船体形状和侧倾角度,观察重点和浮心间的关系。
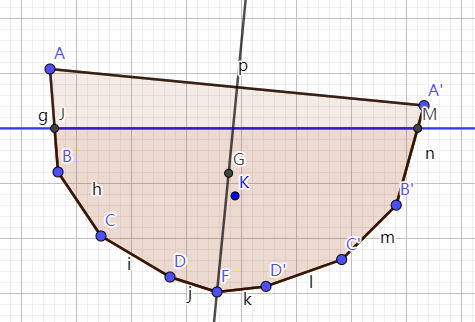
上图中,浮心K用以下多边形求得,由于与水平面相交的边改变了,所以把点L改为点M。

选中船体的多边形,关于重心旋转。如下图所示,绿色多边形是是粉色船体逆时钟旋转45度。
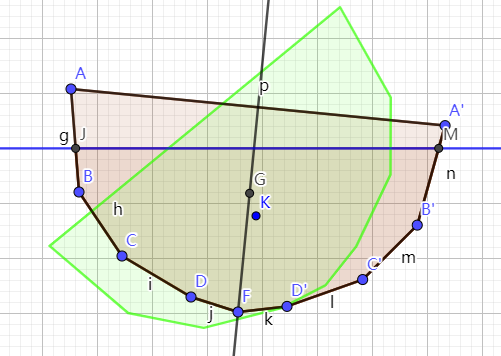
遗留的问题是,船体在重力和浮力的共同作用下,旋转会围绕哪个点进行?
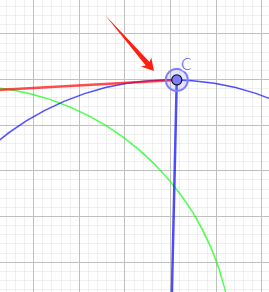
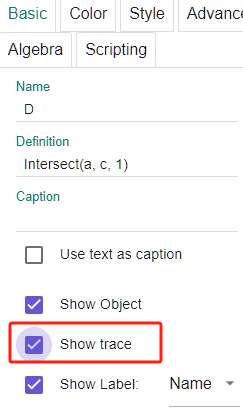
隐藏标签,隐藏无关的元素,改变 caption。截图,标上箭头,如下图所示。
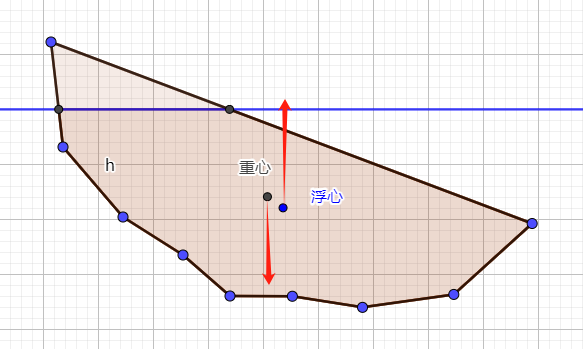
又一个遗留的问题是,重心来自的多边形 比 浮心来自的多边形 多一块面积,即船在水面以上的部分。同时,根据漂浮的船是静止的,浮力等于重力。问题来了,船体面积较大,排开水体面积较小,船体和水体面积不等,为什么分别对应的重力和浮力是相等的呢?
此文也发布在以下站点。
----
知乎 https://www.zhihu.com/people/yang-gui-fu-52
独立博客 https://younggift.net/
微信公众号 杨贵福
----
以下是我曾经发布博客的站点,有些旧文。
----
豆瓣 - 因为审核"我的日记",不再更新。
https://www.douban.com/people/younggift/?_i=0098558fqLUL9h
CSDN – 因为要求我登记手机号码的原因是“为了您的安全”,不再更新。
https://blog.csdn.net/younggift?type=blog
blogsopt – 因为从我的机器不可达,无法更新