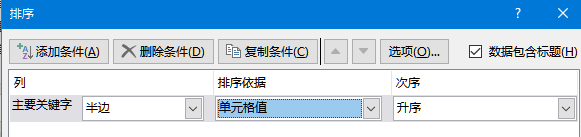
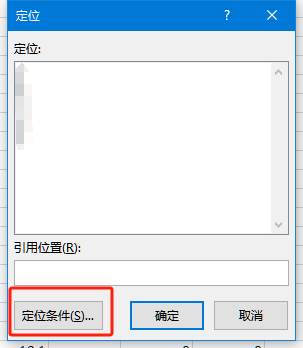
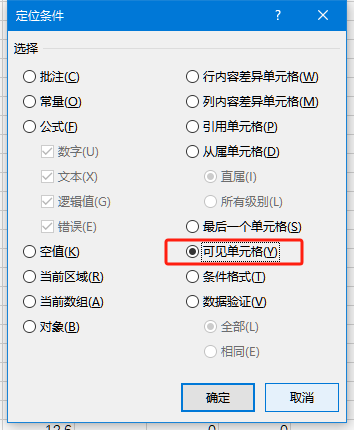
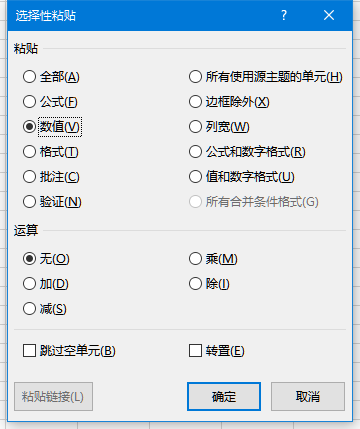
繁体中文的字幕读起来不那么顺畅,转成简体中文就容易多了。对于电视剧有很多字幕文件的情况,需要批量转换。这个实验过程可以帮助理解简繁对应关系、编码,实践命令行工具使用和批处理编写,可以涉及环境变量、搜索路径、cmd和shell知识,以及word、记录本、Total Commander使用。
1. 解决方案
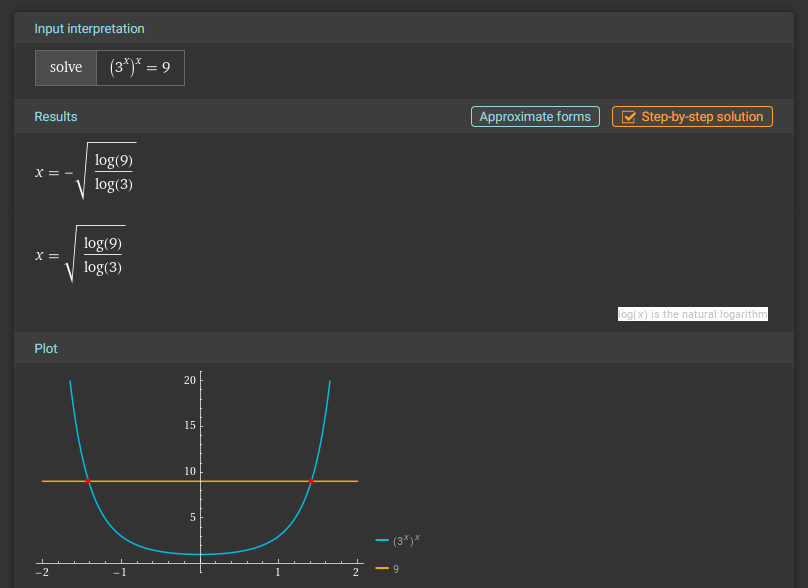
本文把字幕批量从繁体转换为简体,涉及到的命令行工具为 OpenCC 和 iconv。工具的下载路径、简要的原理、其他替代工具将在后文给出。使用如下所示的bat代码。
for %%i in (*.ass) do ( iconv -f UTF-16le -t utf-8 "%%i" > "%%i.utf8" opencc -i "%%i.utf8" -o "%%i" -c c:\tools\opencc\share\opencc\t2s.json del "%%i.utf8" )
2. 繁体转简体,其他工具 及 原理
电影的单个字幕文件转换,可以用word完成。常用的字幕格式 srt, ass 都是纯文本文件,可以用word打开。使用word的"繁转简"功能即可达到目的。
简体 繁體
在原理上,如下图所示,两个“体”字,在同一个文件中可以同时出现。这两个“体”字的的不同并非由于 编码、国别、本地化locale、字体 的差异,而是不同的字符。在编码上互不相关,二者的对应关系完全由于自然语言汉语决定——在技术上,任意两个字符(严格地说,还有多对一、一对多等情况,在此略过)都可以对应——人为规定“体”与“體”之间为简-繁对应。

电视剧的字幕每集一个文件,逐个用word打开操作,有点麻烦。这种任务,一般适合使用命令行操作。
有个 OpenCC 项目,支持命令行下的繁简转换。
https://github.com/BYVoid/OpenCC
我运行时报错,但是没有找到详细手册。猜测 OpenCC 只能读入 UTF-8编码。
![]()
3. 编码,其他工具 及 原理
(1)判定当前编码
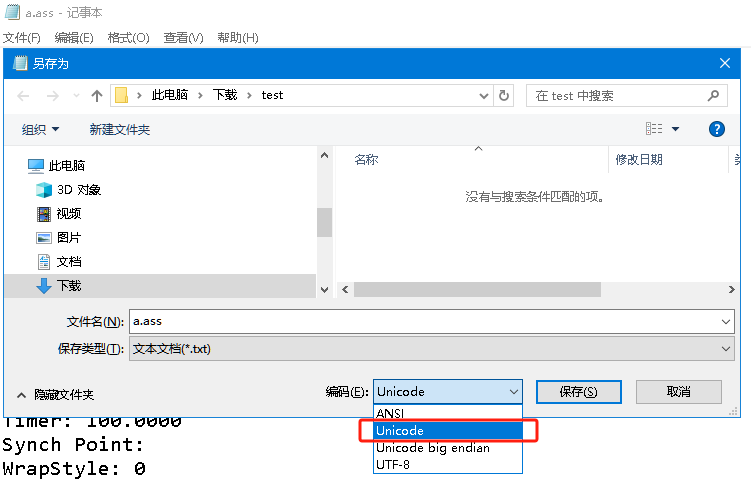
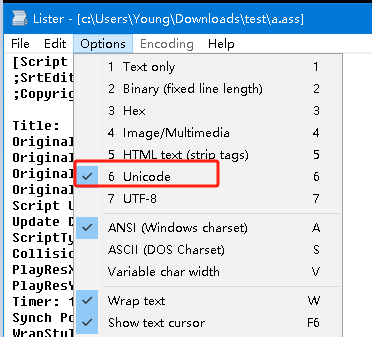
我当前要处理的字幕文件是不是utf-8,查看文件编码可以用 Linux 下的 file 命令。或者用记事本 | 另存为,或者用 Total Commander | F3 查看 等诸多方式。这几种方式间可以相互补充印证。

(2)转换编码
在原理上,编码的不同是更一般性的问题,在各种语言中普遍存在,而不仅在中文中存在。通过 记事本 | 另存为,保存为 UTF-8,可以完成编码的转换,从而符合 OpenCC 的输入条件。也可以使用 SubtitleEdit 另存时转换编码。
批量处理的话,可以使用 iconv。
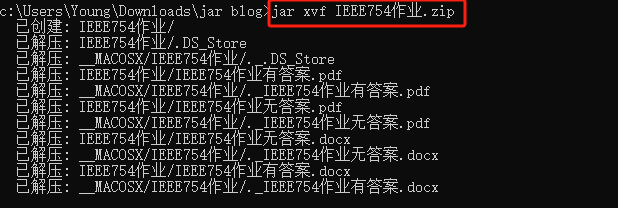
Iconv 在 https://gnuwin32.sourceforge.net/packages/libiconv.htm。下载 Binaries 和 : Dependencies,解压到同一目录中。
4. 批处理
了解以上原理、试用命令行工具对单个文件转换成功后,选用 iconv 和 opencc 写 bat代码 完成批量转换。
(1)遍历目录
遍历当前目录,并以扩展名 ass 作为筛选文件的条件,形成下面的循环。
for %%i in (*.ass) do ( rem 对每个文件执行的操作 )
(2)对每个文件执行编码转换,然后由繁体转换为简体
在循环体中对遍历的每个文件执行类似操作。
第一步,用iconv转换编码,由utf-16 小端 unicode 到 utf-8。
第二步,用opencc执行由繁体到简体的转换。
第三步,删除临时文件。
for %%i in (*.ass) do ( iconv -f UTF-16le -t utf-8 "%%i" > "%%i.utf8" opencc -i "%%i.utf8" -o "%%i" -c c:\tools\opencc\share\opencc\t2s.json del "%%i.utf8" )
其中 %%i 是对应当前遍历的文件名的变量;
c:\tools\opencc\share\opencc\t2s.json 是繁体到简体的配置文件及其所在路径;
%%i.utf8 是临时文件。
Iconv 和 opencc 需要放在搜索路径%path%下,或者像下面这样使用如下绝对路径。

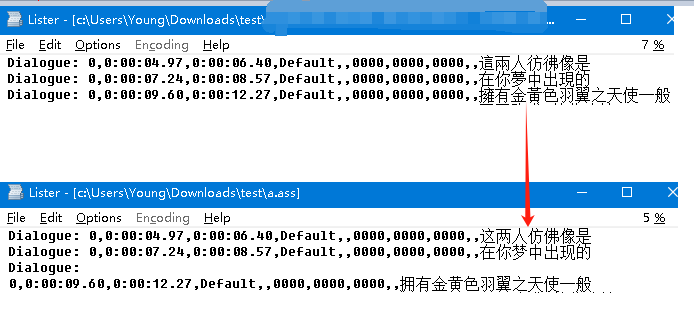
先备份,然后把所有字幕文件放在当前目录下,执行上述批处理(名字就叫“字幕文件 unicode2utf8 繁2简 - go.bat”)。一瞬间以后,所以字幕文件完成了编码和繁简转换。在此案例中,只有一个文件 a.ass。

使用 Total Commander | F3 功能或者上述提到的其他方法,可以验证编码转换完成。

打开文件查看内容,可以检验,已由繁体转换为简体。