发现一个诱人的工具
看到HelloGitHub https://zhuanlan.zhihu.com/p/1888869567515833442 介绍audiblez是个好工具,能把电子书转换为语音,支持汉语和英语。再一查,https://github.com/santinic/audiblez 。基于 TTS模型,大小只有区区Kokoro-82M 。据说转换速度也快,人声也自然。速度可调。
正巧前一段时间微信读书禁了私有图书的朗诵功能,这工具不就来了么。
准备装一个,以下就是流程。
流程之所以值得写下来,当然足够丰富多彩、跌宕起伏、扣人心弦。
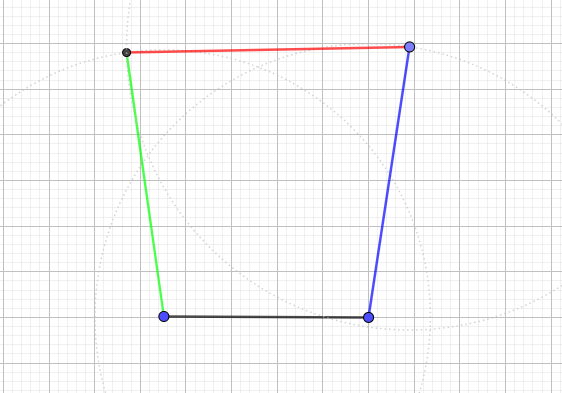
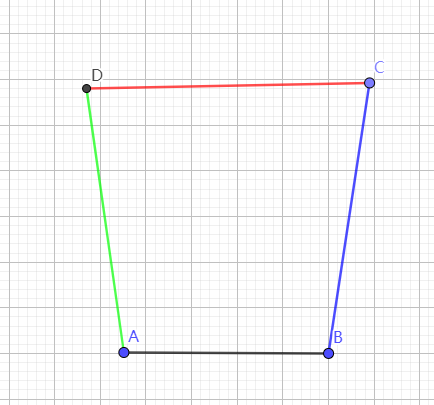
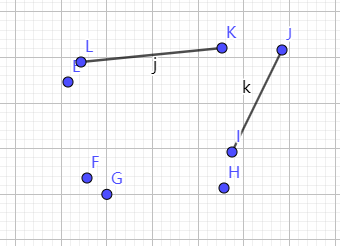
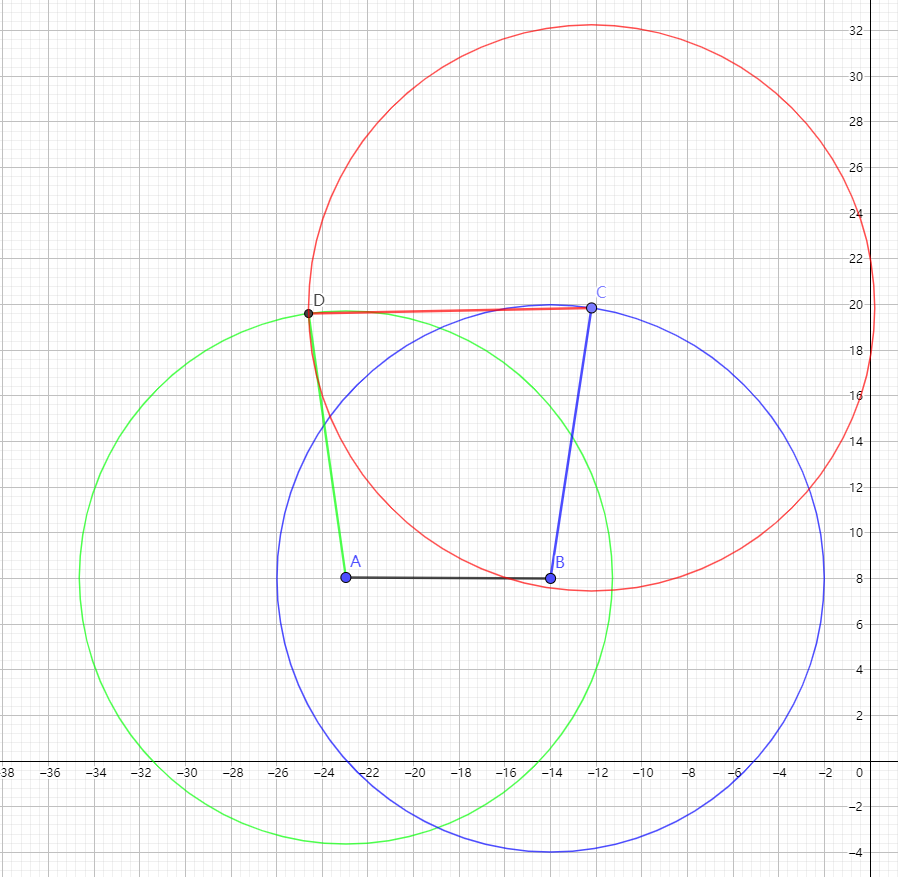
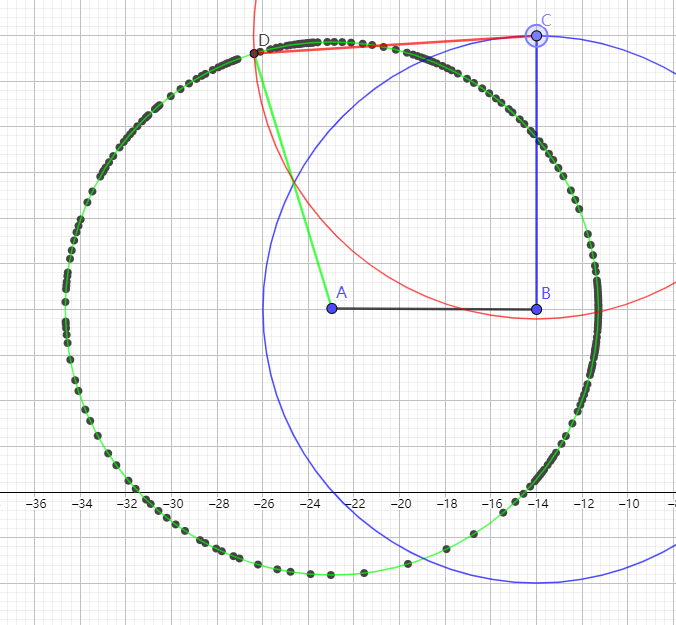
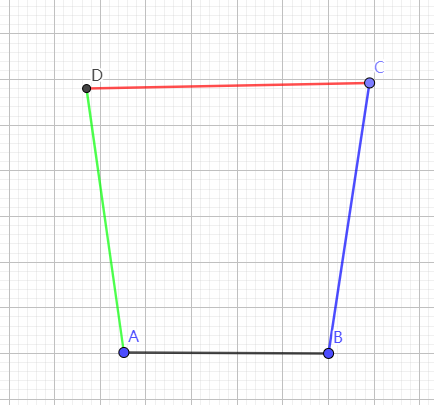
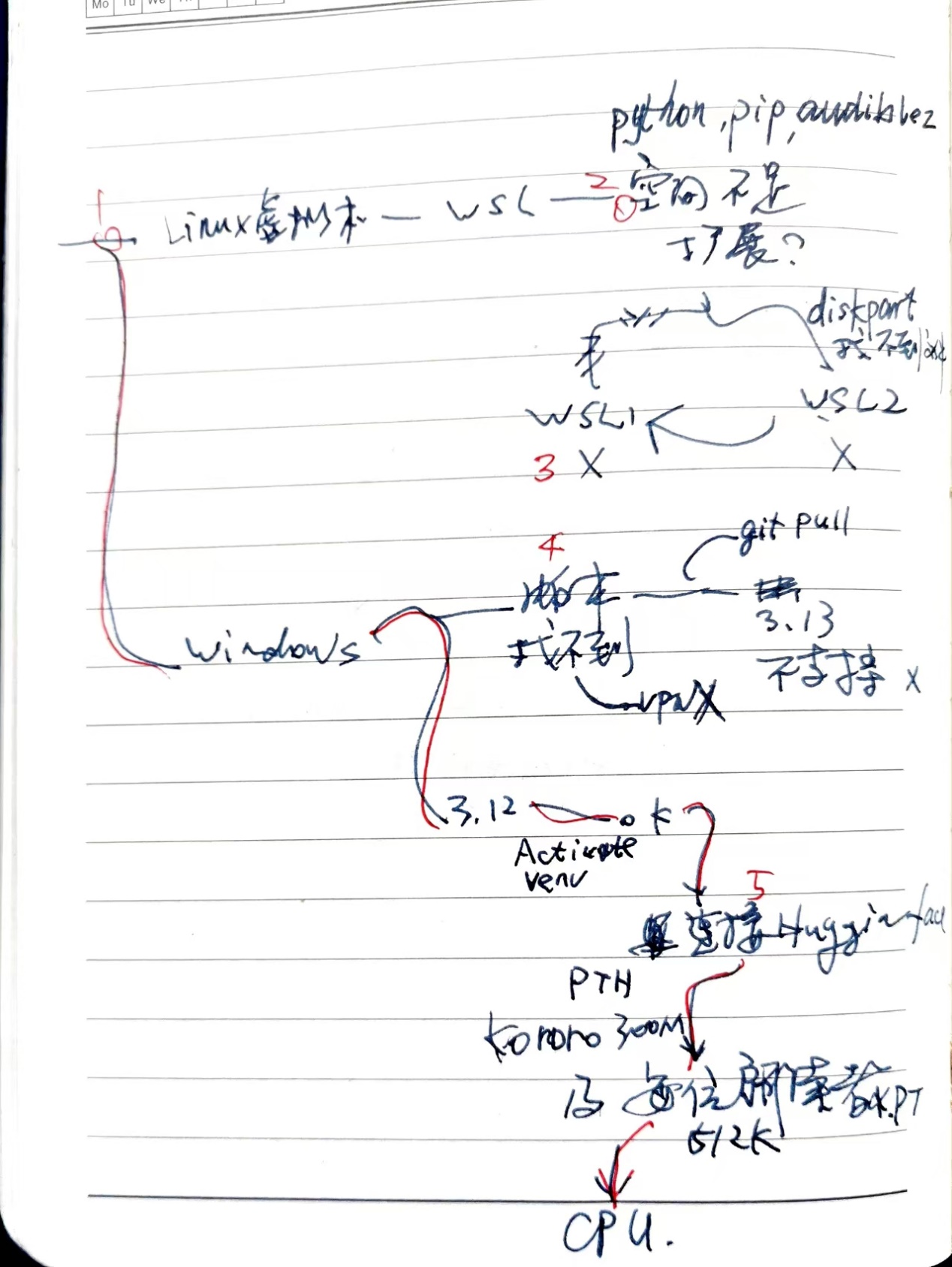
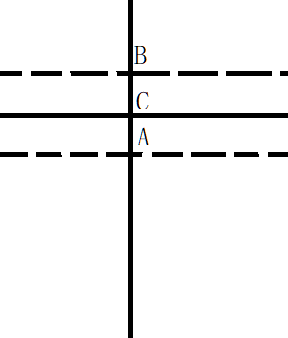
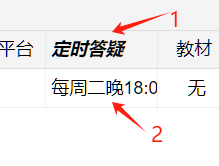
事后总结的路线图如下。我们现在前进到数字1处,在左上角。
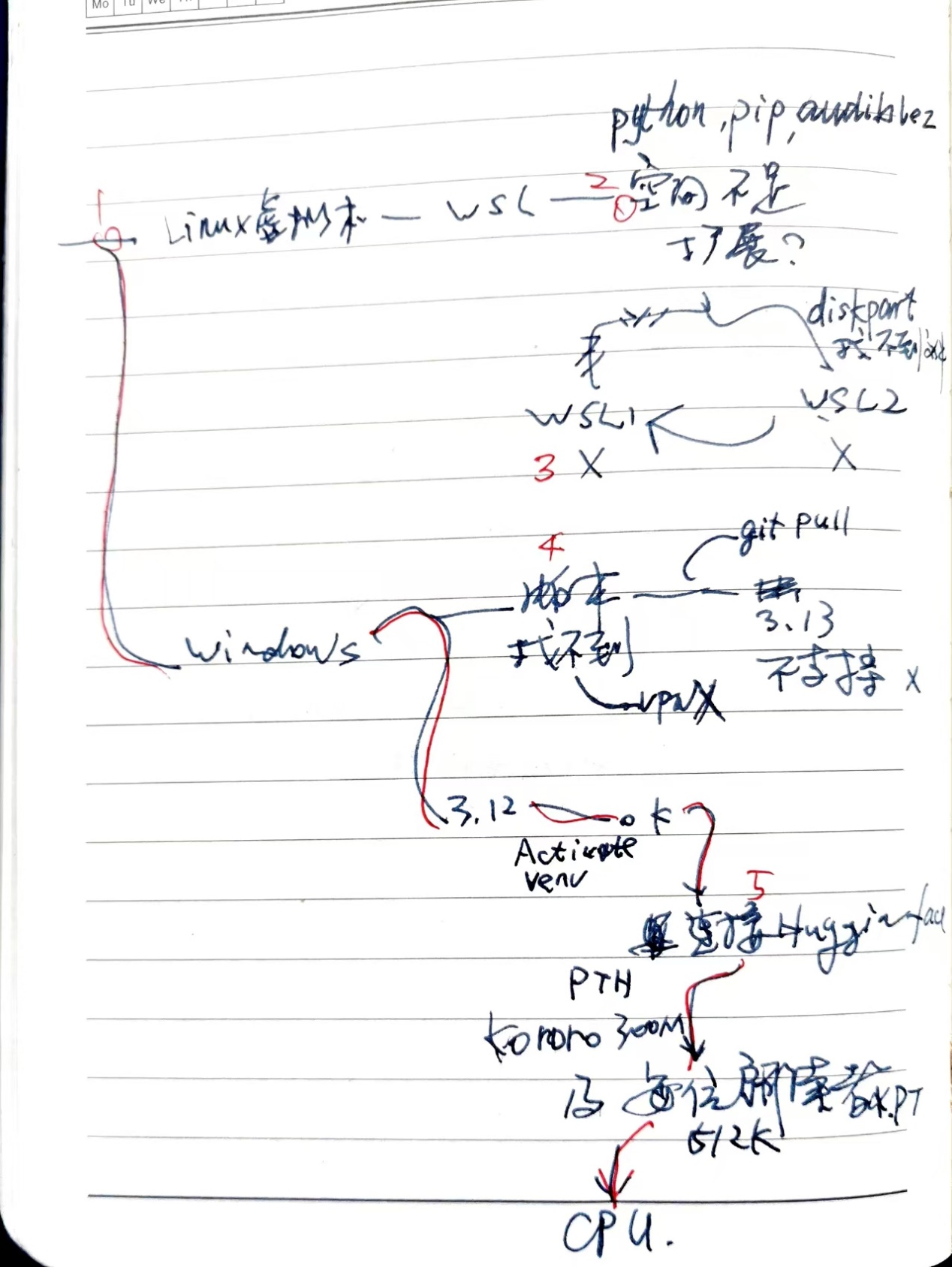
安装节点1 Linux还是Windows
Audiblez基于 python,按说应该是跨平台的。为什么还要区分操作系统呢?因为官方的 readme 里 https://github.com/santinic/audiblez 提到了。
把整个工程从 github上pull 下来,只有9.7M,其中示例的声音文件8.7M,截屏图1张600多K。代码43K,测试12K。
用wc统计一下行数,代码部分共1000多行,测试部分不到300行。
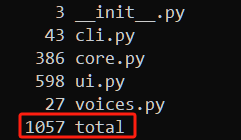
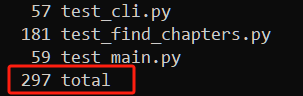
看到这里,是不是有雄心自己写一个?
这么少量的工作,安装一定不复杂吧。我不禁这样想道。
我的机器是 windows,刚好装了 wsl,有ubuntu。就装在这里吧。
手册中涉及到这部分的内容非常简洁。

中间发现没有python等,我又安装了 python, pip, venv。
这部分没有记录日志,因为一切顺利。
在安装audiblez时,系统报 空间不足。见面图,我们此刻前到 数字2处,在右上角。

安装节点2 空间不足
空间不足怎么扩展呢?查一下。
https://learn.microsoft.com/zh-cn/windows/wsl/disk-space 说,关闭wsl的分发,可以理解为把虚拟机 ubuntu关闭。
咦,日志里好像都关了?wsl.exe –shutdown
总之“关机”,一切顺利。
要运行 diskpart 命令行,调整ubuntu所在的虚拟文件的大小。为了调整这个文件的大小,要先找到这个文件。https://learn.microsoft.com/zh-cn/windows/wsl/disk-space#how-to-locate-the-vhdx-file-and-disk-path-for-your-linux-distribution 如是说。
PS C:\Users\young> (Get-ChildItem -Path HKCU:\Software\Microsoft\Windows\CurrentVersion\Lxss | Where-Object { $_.GetValue("DistributionName") -eq 'Ubuntu' }).GetValue("BasePath") + "\ext4.vhdx"
异常现象,在我的机器上找不到这个文件。
我用everything 搜索 ext4.vhdx,不仅 ubuntu 的没有,我的机器上没有任何 ext4.vhdx 文件。
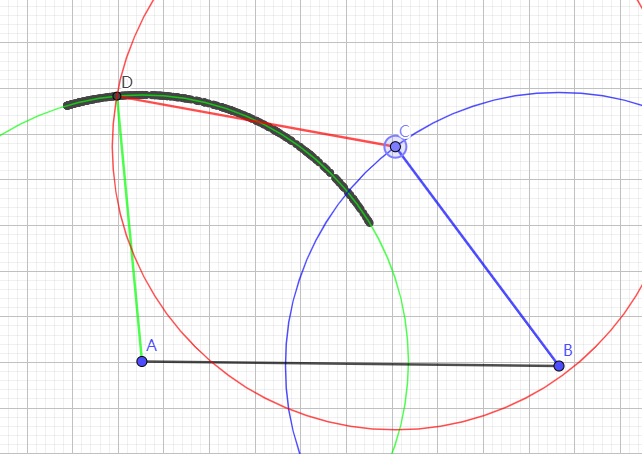
在下图中,我们马上将行进到数字3的位置,在右侧中间偏上。
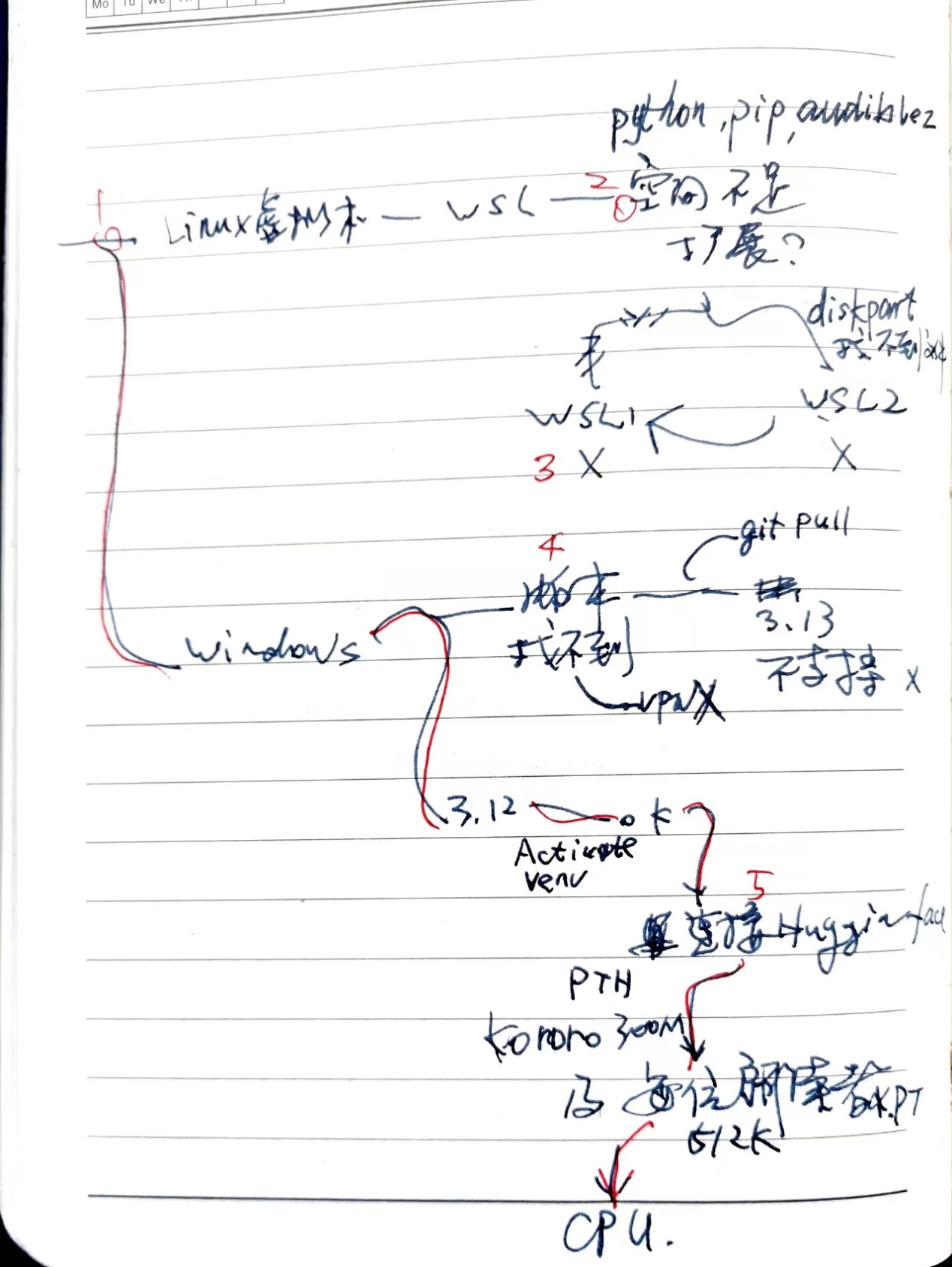
安装节点3 WSL1还是WSL2
再查理论细节,我知道装了wsl,是只知其一,不知其二。当初装wsl也费了不少周折,主要原因是微软的手册的目标读者可以访问的地方,我不可达。周折如此之多,以至于我已经完全忘了选择wsl1还是wsl2这个步骤。甚至不记得还有wsl1和wsl2的区别。
再查知道wsl1没有使用虚拟磁盘,这能解释我查不到ext4.vhdx文件。那么,wsl1如何扩展磁盘空间呢?不需要特殊操作,因为wsl1使用宿主机操作系统的磁盘空间。我明明还有3G多空间,你不是只需要80多M吗?
我wsl到底是1还是2呢?有的说1,有的说2。
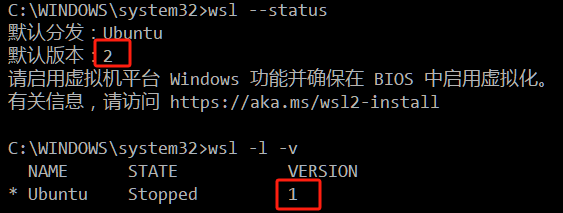
也许wsl是2,ubuntu是1。
ubuntu装了半巴拉卡的python+pip+venv+audiblez,报空间不足,其实有空间。够了!我不想知道为什么了。我把ubuntu删除,以后用的时间再装吧。
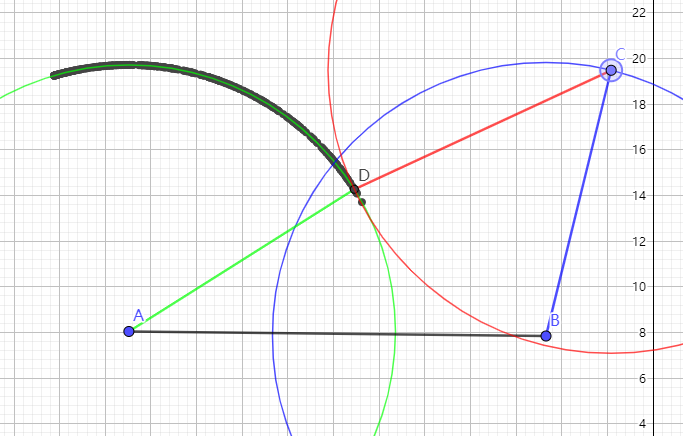
进入下一步,我们现在前进到数字4,在下图的右侧中间。
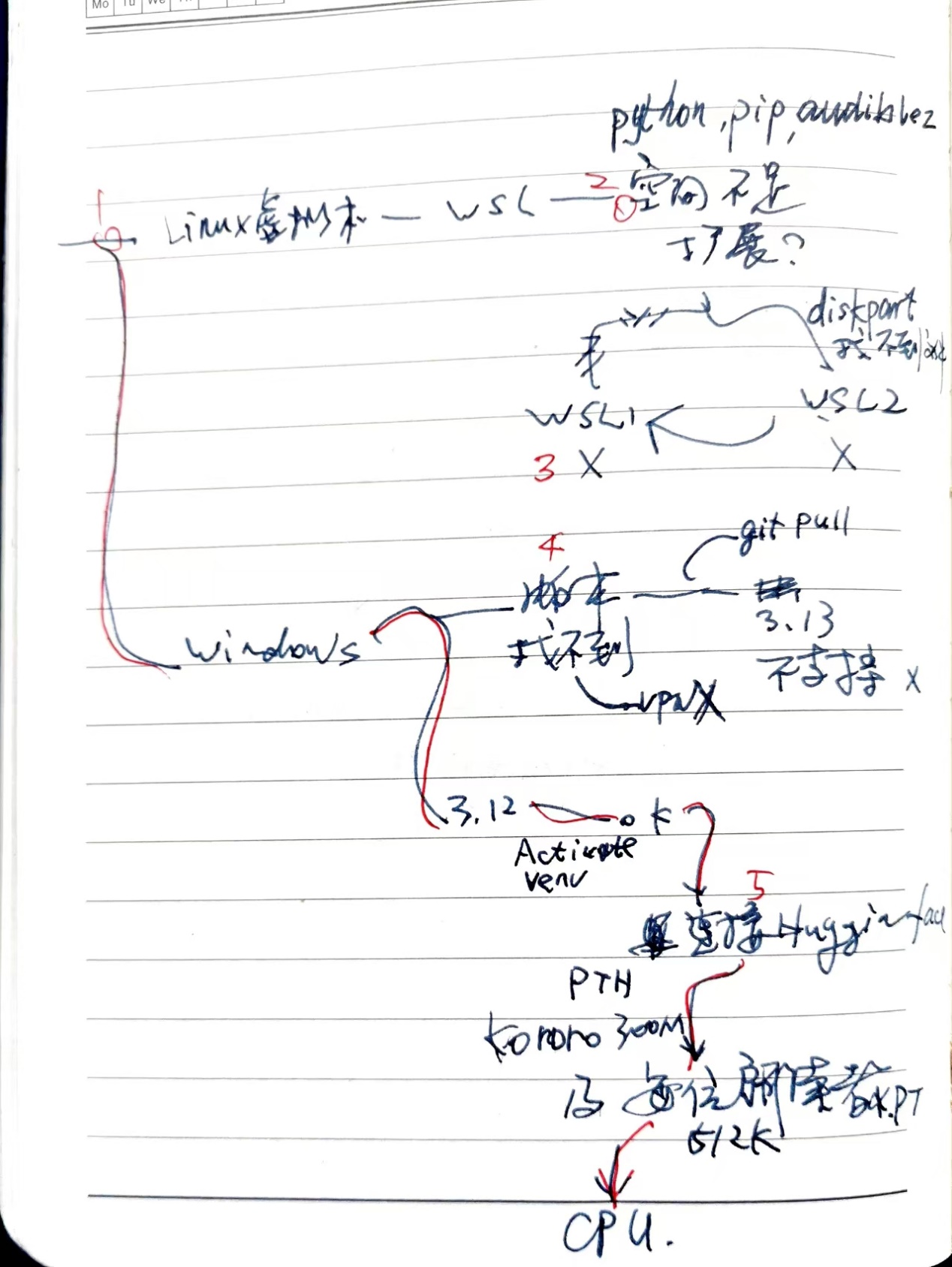
安装节点4 pip找不到匹配的版本
开始Windows操作系统下的安装。手册上看起来比 linux 下要复杂一些,难度增加有限。感觉如此。
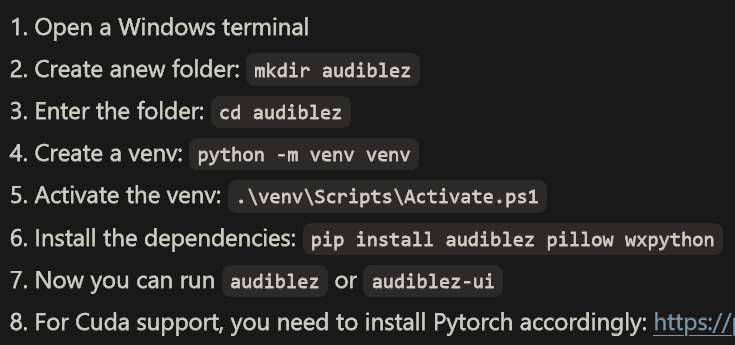
打开 Windows terminal,这是什么东西?cmd,还是 powershell,还是开个 bash?看第二步,我会,可以跳过第一步。边读边操作,我心里不禁碎碎念,麻烦的你不解释,简单的偏偏要说上两嘴。
作者假设我装了python。我只好装上,让他的假设成真。这样一路在cmd里就到了第5步。运行这个ps1以后,打开了一个记事本。这肯定不对啊。我切到 powershell 下操作。现象如下。

我还没从删除ubuntu的余怒中恢复,不想读。
搜索一番,切到cmd,运行activate.bat。我心想,就设置个环境变量,让你整得这么麻烦。
这就到了第6步 pip install audiblez 等东西。
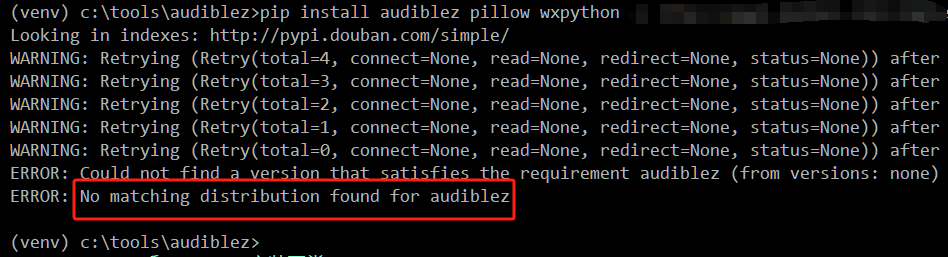
一定是因为我不用VPN,我大声咒骂。
我开始尝试换各种镜像数据源,都是网上的邻居家随便谁说的,准确性和安全性完全无法保证。谁让我连不上互联网呢。
-i http://pypi.douban.com/simple/ --trusted-host pypi.douban.com
不行。
你可能试着用VPN连一下。不行。大声咒骂。
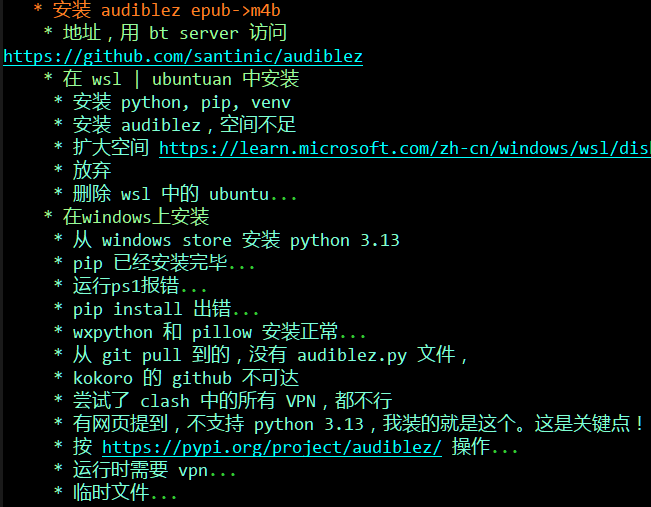
wxpython 和 pillow 安装正常,只有 audiblez 找不到匹配的。
我放弃了一会儿,遍历所有与 audiblez 有关的贴子。有的非常早,是它的上一个版本,只有一屏代码,调用 Kokoro-82M 的。这是要逼着我照着写一遍?我能下载到Kokoro-82M吗?放着能用的开源不用,非要单独自己搞一套。我是不是有病?大声咒骂。
骂人的同时不影响我继续遍历这些贴子,终于看到了救命的。https://www.aisharenet.com/audiblez/ 在需要先安装 python3的旁边说 python 3.13不行。
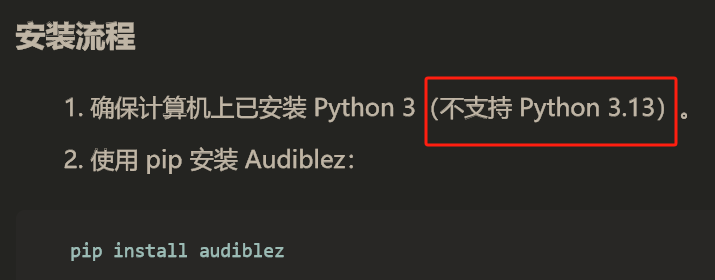
我已经看过30篇左右贴子了,都提到 python 3,不记得3.13不行。而且,我装的就是 3.13,觉得既然要求 python 3,那么 3.13也是3,并且够新。作者提到过3.13不吗?作者确实没有提到3.13行,但是他也没能提到3.13行。他说3.9~3.12。

卸载 python 3.13,安装 python 3.12。再回到第6步,记得我们在哪里吗?
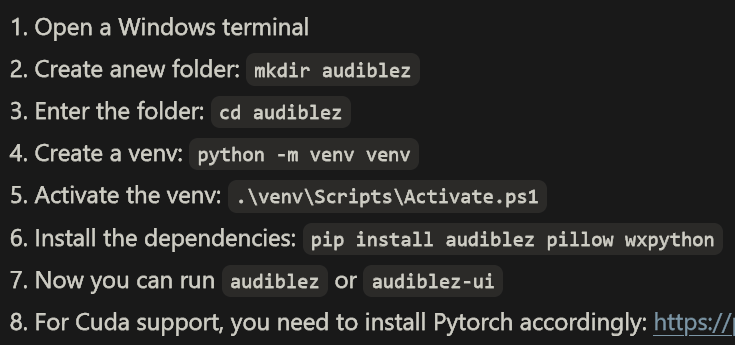
一切顺利,花了相当长时间,不断地从网上下载东西。

原来,这1000多行虽短,它依赖的东西可真不少。有这么多。
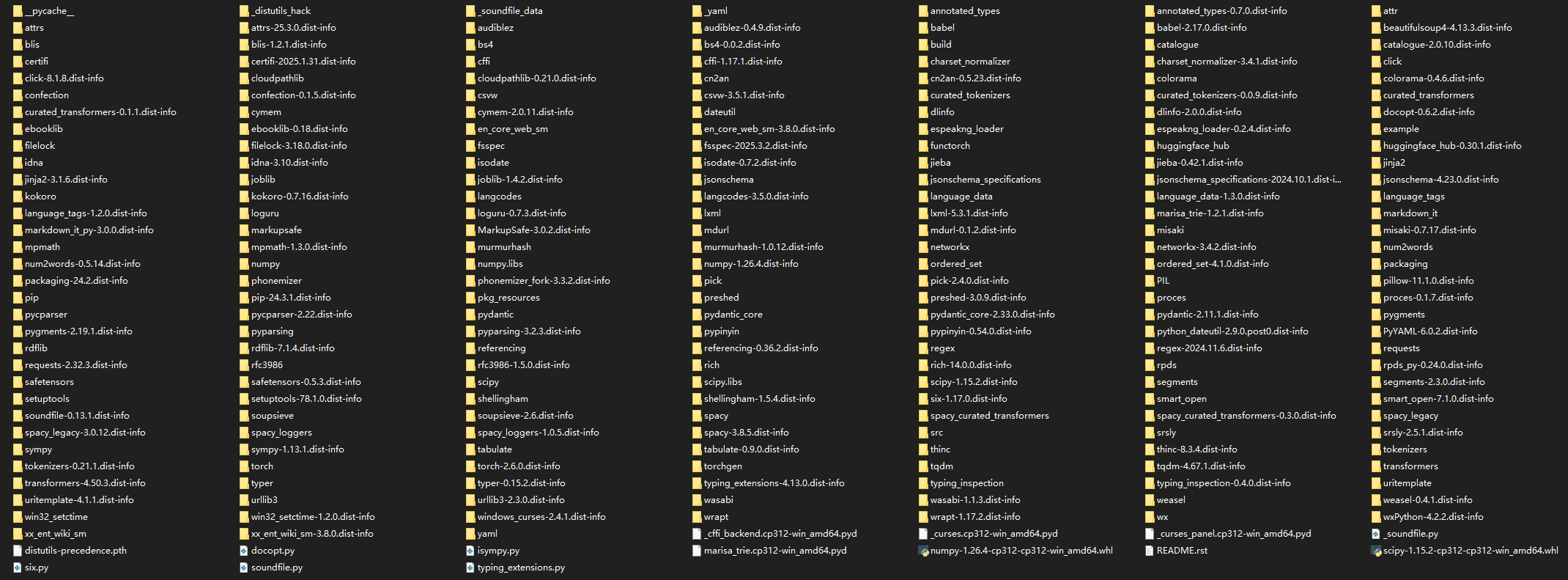
看到了很多熟悉的名字 torch, scipy, transformers, spacy, sympy,wx……依赖200多个“子”项目,共占空间 1.92 GB (2,064,649,065 字节)。Kokoro-82M。82M?我幼稚了。
我们到了下图中的数字5,右下角附近。
安装节点5 要连接互联网
接下来第7步,运行 audiblez-ui。
我在控制台上看到字符翻滚,扫到一眼“你需要连接互联网”。说什么胡话呢?1987年我们就走向世界了。

总之,连接互联网,我发现 audiblez-ui 在运行时下载东西。
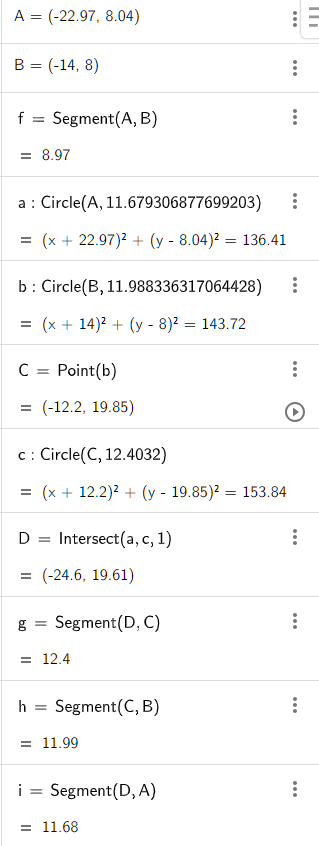
从huggingface 下载了317 MB (332,448,853 字节)东西。其中kokoro-v1_0.pth占319M。就是它了,kokoro 82M。虽然kokoro 82M高达300多M,但是和刚刚安装的1.9G相比,也算不了什么。
成功。
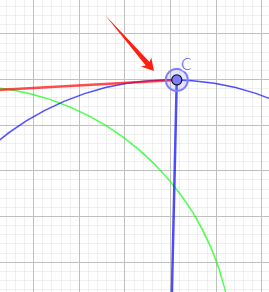
打开一本电子书,预览声音。又开始连接互联网。每个不同角色的音色,会下载 名如zm_yunyang.pt 的文件,500多K。不大。但是如果每次都要连接互联网,相当麻烦。
![]()
此时,我大声咒骂。同时,对外国开发者不考虑我辈的困难……我能说什么呢,想起了有人提到,光荣公司为什么不做简体中文的三国志。
测试,好在,这些角色的文件是可以缓存的。在这里
c:\Users\young\.cache\huggingface\hub\models--hexgrad--Kokoro-82M\
效果
我试着转了两本书。
一本英文书,377千左右字符,42章左右。一本中文书,410千左右字符,42章左右,奇数章短,偶数章长。
转换持续了一夜,大约6小时左右,时间不准确。我没有GPU,CPU负载持续85%以上。金属机壳,CPU发烧导致机壳持续50多度。
每章生成一个 wav文件。手册说会转换成 m4b 文件。我的两个测试都失败了。一个文件非常小,另一个进度100%但是m4b文件没有生成。

我用ffmpeg手动把 wav 转成了 mp3。英文这本90多M,中文这本200多M。
声音效果很好,可以与微信读书比美。中文我用了 zm_yunyang,男性普通话。英文用了 af_alloy,美式英语女性。这两位都语调正经。其余的我试了几位。两个中国人,女性,有明显的口音,东北辽宁的和西北的。zf_xiaoxiao,zf_xiaoyi 是普通话。zm_yunjian,zm_yunxi 男性。zm_yunxia 小男孩。
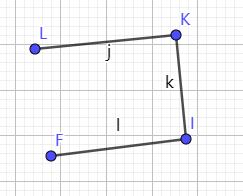
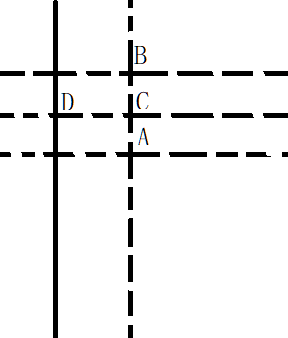
回顾安装的过程,如下图。如果我沿着红线前进,而不是按数字走,会快很多吧。然而,当时,我并不知道应该朝哪个方向走。树多歧而路多枝,你不试试如何知。有些人可能会快很多,不走弯路。有的是理论功底好,猜得准;有的是刚好见过这个故障,知道原因;有的他出生在罗马,不必怀疑网断了,也不必为猜错了浪费时间。
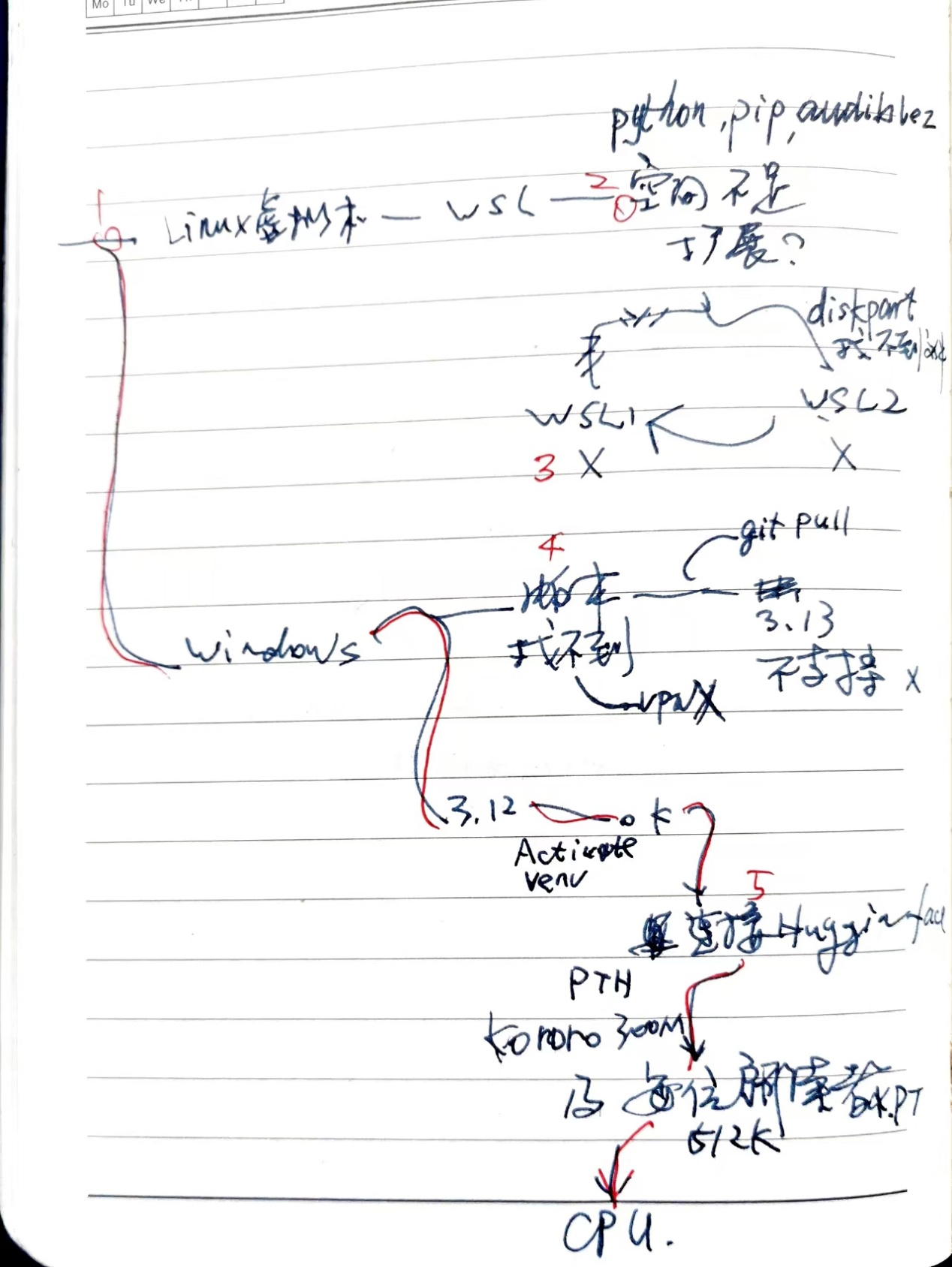
我只能一步一个脚印记录。如果你遇到的现象刚好与我相同,也许有所帮助。
我想把声音和视频放在这里,请你感受一下自然流畅的语音,还有把电子书拆成章节的功能。我想了一下哪些书没有版权,适合展示,想到了几本中文的,想到了几本英文的。最终选定了这个贴子本身。有些不好的效果可以想办法去除,不过我保留原样,也算展示这个工具不完善之处。你还是自己安装试试吧。
demo
此文也发布在以下站点。
----
知乎 https://www.zhihu.com/people/yang-gui-fu-52
微信公众号 杨贵福
----
以下是我曾经发布博客的站点,有些旧文。
----
豆瓣 - 因为审核"我的日记",不再更新。
https://www.douban.com/people/younggift/?_i=0098558fqLUL9h
CSDN – 因为要求我登记手机号码的原因是“为了您的安全”,不再更新。
https://blog.csdn.net/younggift?type=blog
blogsopt – 因为从我的机器不可达,无法更新


























































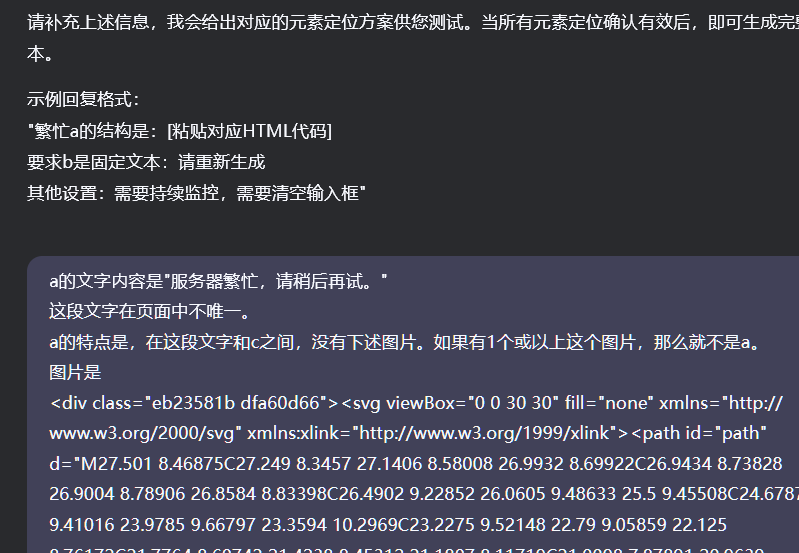

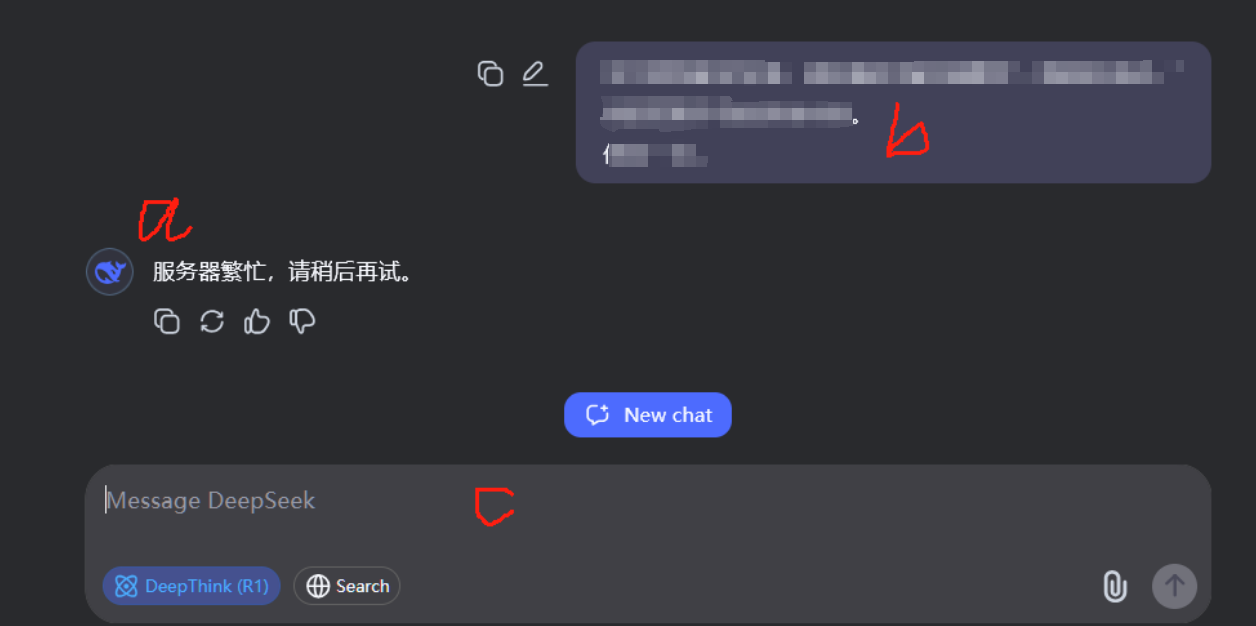




 ,还是这样
,还是这样  ?
?