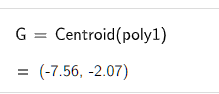
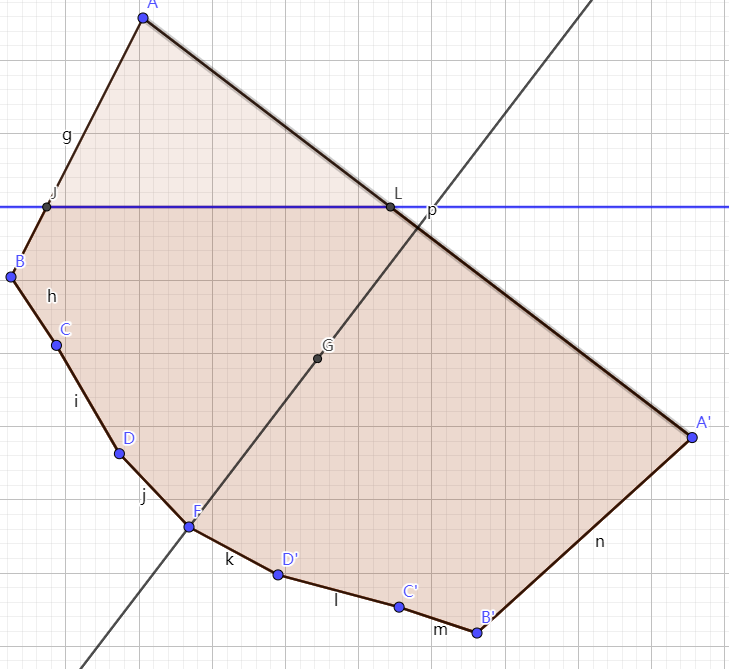
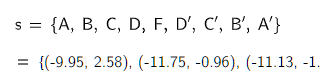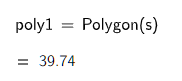以下,是2024年12月16日晚在东北师大图书馆本部读书分享《科幻与我》的一段,感谢王文佳老师邀请。现回忆写成文字,投稿到河流老师的征文《我与科幻》,并发在我的博客上。
很久以后,我们才知道当初的某件小事的意义深远。读书经常给我这种感觉,读完跟没读一样。但是那一页不知不觉已经长久深刻影响着我,二三十年后的某一刻才突然知道,当时读得居然是它啊,怪不得。
学前我没有上过幼儿园,不认字。上小学之前,我爸教会我写“岳飞”两个字,还有我自己的名字。都是繁体的,其中的飞字我当时写得张牙舞爪,我爸评论“真飞起来了”。
不认字,当时也没有漫画,只有小人书,印象最深的有两本。一本是《英雄救日月》,也许西南一带,也许东南亚或南亚的民间故事。画风充满装饰意味,非常现代,色调黑白对比鲜明。故事是蛇妖偷走了太阳和月亮,英雄把它们救了回来,并且顺带把蛇妖一家灭门了的故事。我哥带我捞泥鳅的时候,我们把所有大小泥鳅都安排了角色,就是蛇公蛇母蛇祖蛇孙。这为我们涸泽而渔的行为赋予了正义的意义。另一本是《变法斗三仙》,西游记一整套里的一本,讲的是师徒四人和虎力大仙、鹿力大仙、羊力大仙斗法的故事。线描风格。有剖腹挖肝、在大锅里煮人这样的情节,还有人被虫子蛰从高台上掉下来。破烂流丢一口钟,也是这里的。那么多小人书,《铁腿红心》《人民医生李月华》内容都没多少印象了,偏偏记住这两本。可见少年天性,耽于幻想,长大以后看电影只喜欢打打杀杀看不懂情情爱爱,一直以来对现实主义的兴趣就不大。
也有些我爸读给我和我哥听的。家里还有半部《三国演义》,我爸从市图书馆借的《陈十四奇传》。后面这本是非现实主义作品,给我的印象比三国要浓烈。长期以来我常记成《陈十四传奇》,讲一位剑仙女士,名字叫陈十四,也许不是剑仙而是学了别的法门。性别不会错,总之很厉害。她和蛇妖斗争的故事。咦,为什么又是蛇妖?胜了。最后还剩了三寸蛇尾,居然也能兴风作浪,双一顿打斗。这位女士的儿子也有法术血统,剪了小纸人儿把他的爸爸从床上抬起来扔地上。这儿子的爸爸,也就是陈十四的丈夫,是个县官。
除了这些,还有我哥订的杂志。《看图说话》和《东方少年》,好像是这个名字,印象不深了。有个杂志叫作《智慧树》,其中一篇《钩吻》给我留下深刻的印象,我哥读给我听的。神农氏尝百草的报告文学版本,附图是那种很扭曲而有美感的画风,现在看也许从汉墓引申而来。神农氏最后尝到的草药就是钩吻,吃了以后他看不见听不到,肚子也疼。经过很多痛苦,痛苦的细节文中有写,也令儿童时代的我深受震撼。后来他死了。我的同龄人很多第一次知道钩吻,即断肠草,是从《神雕侠侣》里知道的。读到医生向杨过科普钩吻的时候,我心里想的是,这个我知道,你没救了。
除了这些,日常最容易接触到的阅读材料是 日历牌。不是挂历,有点像黄历,每页是单独的一天,平日黑色,星期六绿色,星期天红色。每页除了年、月、日、农历以外,下面还有三四行小字,科普常识。没有宜忌之类的。这是我科普阅读的开始,一直到初中,我姨家的妹妹还替我攒了不少等着给我。
我哥给我讲过狭义相对论。尺缩效应,在很长的街道上,以接近光速行走,长剑像铁钉一样短。人不能超过光速。我问,如果用一个小齿轮,套在另一个非常大的齿轮上。小齿轮转得接近光速,大齿轮不就超过光速了吗?我哥说,齿轮就爆了。这段对话发生在我小学三四年级以前,我哥初一以前。
以上这些,在我看来都是广义上的科幻。阅读,也只能接触到这样的狭窄范围。
 除此以外,就是广播。中央人民广播电台,孙敬修老爷爷,“小喇叭开始广播啦,dadida”。通化人民广播电台,330米909千赫。听过不少广播剧,每个都不止一遍。《远山没有雪》,一对苦命知青在西南一带下乡,女青年后来成为东南亚游击的骨干,她一直介怀“远山没有雪”。一部忘了名字的广播剧,讲几个科技工作者在长白山采集气象资料。要过某个山口的时候狂风大作,大雨或大雪倾盆而下。一个女青年吓得大喊,“这座活火山是不是要喷发啦?”熊的吼叫。真由美和探员吓得尖声喊叫,“熊!”杜丘冷静的声音,“熊。”东京街头闹市区的奔马群,啦呀啦的歌声。真由美说,“这就完了吗?”杜丘说,“哪有个完呐。”还有温和的男中音讲《梦游天姥吟留别》。也许这是在我识字以后的事情了,不过,我一定是先听到后读到,因为“姥”字不会读错。还有讲《春江花月夜》的,广播剧提到雨果的。
除此以外,就是广播。中央人民广播电台,孙敬修老爷爷,“小喇叭开始广播啦,dadida”。通化人民广播电台,330米909千赫。听过不少广播剧,每个都不止一遍。《远山没有雪》,一对苦命知青在西南一带下乡,女青年后来成为东南亚游击的骨干,她一直介怀“远山没有雪”。一部忘了名字的广播剧,讲几个科技工作者在长白山采集气象资料。要过某个山口的时候狂风大作,大雨或大雪倾盆而下。一个女青年吓得大喊,“这座活火山是不是要喷发啦?”熊的吼叫。真由美和探员吓得尖声喊叫,“熊!”杜丘冷静的声音,“熊。”东京街头闹市区的奔马群,啦呀啦的歌声。真由美说,“这就完了吗?”杜丘说,“哪有个完呐。”还有温和的男中音讲《梦游天姥吟留别》。也许这是在我识字以后的事情了,不过,我一定是先听到后读到,因为“姥”字不会读错。还有讲《春江花月夜》的,广播剧提到雨果的。
广播里还有京剧,所以收音机本名戏匣子。京剧我一句也不理解,我姥爷甚是喜欢,我对他的喜欢也不能理解。学前在我姥家还看了不少电视,有相当多片断当时完全不懂,后来让我一拍大腿“原来是这个”的那种。
我记得的,大部分是“一个小男孩”开头,因为只能看懂这种。一个小男孩,为了挣钱为带到一个大城堡里。里面黑乎乎的,只有蜡烛。有个老太太穿着大袍,装饰繁复,在烛光下闪光一样。有个小女孩照顾老太太。老太挺吓人,小女孩也严肃得很。后来我读某本书的时候,感觉非常诡异,就是那种“我在哪里见过这个妹妹”的恐怖版本。我读过?没有啊。但是为什么有印象。直到后来慢慢回忆丰富,嵌入在十二寸还是九寸黑白电视里,一切才清晰起来。这是《远大前程》。
一个小男孩,被派为栅栏刷油漆,骗了一群小朋友替他刷。一个小男孩,带着一个大姐姐,陷在一个溶洞里。很多年以后读书时发现这是《汤姆·索亚历险记》。所谓大姐姐就是我当时的看法,类似我小学一年级,看到我们班主任把她家孩子带到班级,说“打预防针非常好,你们看我把自己孩子都带来了”。我们老师的孩子当时在我看来就是非常大非常能打的大姐姐。现在看,也就是初高中生。
一个青年倚在燃烧的巨大车轮上,用纸笔写着什么。衣着华丽,像中世纪的贵族。远处士兵们还在拼杀。似乎有炮声和马嘶。很多年以后,在《战争与和平》里我又一次看到了这一幕。
小女孩被送到她爷爷或者姥爷那里生活,用非常粗糙的毛市,洗脸盆是巨大的石头槽。远处有巨大巍峨的高山,我的印象里那是安第斯山或者落基山。都不是。后来跟二猫一起看电影的时候,我一拍大腿,“这个我看过!”是阿尔卑斯山,《海蒂与爷爷》。
当时居然有机会看到这么多名著。
还有,和丹麦的Lars教授和Anders教授聊起来老电影。他们的年龄都要比我大二三十岁那样吧。我们聊起《西部往事》,提到哥哥被坏人在脖子上挂着绳子,站在弟弟的肩膀上,后来弟弟撑不住,眼睁睁看着哥哥吊死了。按说,我小时候的年代,应该没有机会看到这部美国影片才对。但是情节完全对应,只能用看过解释。又过了十来年,有同事听我讲这个,告诉我,你看的是另一部,印度影片,也有这个情节。当时我有一种科幻迷遇到刘慈欣、燕垒生、宝树的感觉,他们什么都知道,你提个头儿,他就告诉你这个头儿的几个来源,然后就能讲下去了,涛涛不绝。印度影片,这就解释得通了,而且我可能是在电影院看了。这部影片的名字,我找到过,又忘记了。
后来,上学以后,就识字了。有市图书馆,小学、初中、高中,学校都有图书馆室。可以有更大的阅读范围。同学也识字,同学的家里也有很多书。
在于波、李国志、张海旭、赵志刚中某位同学家里,第一次看到《星球大战》,有人对主人公说“我是你爸爸”。我们画了不少设定,肚子里的三维指南针之类的,考虑它们的实现需要哪些技术。很多年以后在录像厅里第一次听到这段话,原来是这样的声音,在这样的场景。我久远以来的记忆,那些模糊得看不清样子的记忆,已经不知道与这真实的场景有哪些差异了。
在陈军同学家里第一次看到《星际迷航》,我相当长时间猜测外星飞船的名字是 维吉尔,古罗马诗人,看到最后才知道是Voyager,第一个飞出太阳系的人类造物。这本书沉在我的大脑深处,久无印象,看到看电影《星际迷航》第一部分。又是那种感觉,我看过这个。到了大揭秘的时候,我慨然长叹,是你啊,老友。
老友。就像莱茵哈特称呼齐格飞的那句墓志铭。吾友,Mein Freund。
那些机缘最终把我们引导到如今的这条道路上。很久以后的现在看来,宿命一般,虽然大家宿命的路线差异巨大,但是最终塑造成有机会相互阅读的彼此。
此文也发布在以下站点。
----
知乎 https://www.zhihu.com/people/yang-gui-fu-52
微信公众号 杨贵福
----
以下是我曾经发布博客的站点,有些旧文。
----
豆瓣 - 因为审核"我的日记",不再更新。
https://www.douban.com/people/younggift/?_i=0098558fqLUL9h
CSDN – 因为要求我登记手机号码的原因是“为了您的安全”,不再更新。
https://blog.csdn.net/younggift?type=blog
blogsopt – 因为从我的机器不可达,无法更新